Historie
History is currently empty

    Přihlaste se, abyste využili všech funkcí

    • Historie výpočtů
    • Uložit a synchronizovat nastavení
    • Využívat pokročilé funkce
    Proměnná

    Komplexní průvodce vědeckými kalkulačkami

    1. Úvod

    Vědecká kalkulačka je výkonný nástroj určený pro složité matematické výpočty, které daleko převyšují schopnosti standardní kalkulačky. Nejenže provádí základní aritmetické operace, ale i pokročilé funkce důležité pro vyšší vzdělání, inženýrství, vědu a matematiku. Vědecké kalkulačky jsou neocenitelné ve vzdělávacích a profesních prostředích, kde pomáhají studentům a profesionálům s přesnými výpočty.

    Skutečná vědecká kalkulačka

    Kromě fyzických kalkulaček je na naší webové stránce k dispozici i pohodlná online vědecká kalkulačka. Tento nástroj zrcadlí funkce tradičních vědeckých kalkulaček a přidává výhodu přístupnosti z jakéhokoli zařízení připojeného k internetu, což zajišťuje, že výpočty máte vždy po ruce. Vědecká kalkulačka online 991 Plus je pokročilá verze nabízející širokou škálu funkcí vhodných pro složité matematické operace, uspokojující potřeby studentů, pedagogů a profesionálů.

    Online vědecká kalkulačka

    2. Klíčové vlastnosti vědecké kalkulačky

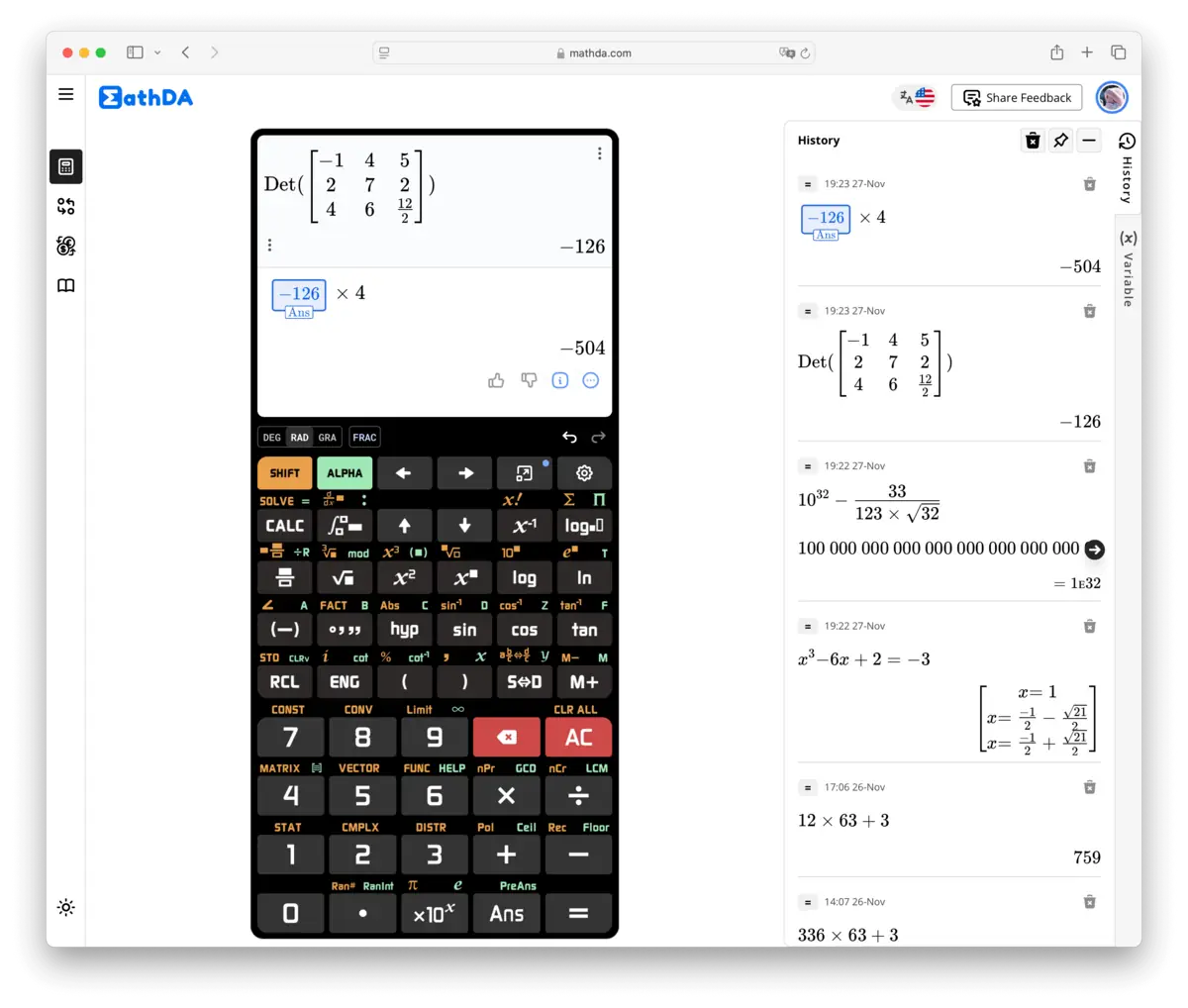
    Vědecké kalkulačky jsou vybaveny řadou funkcí, které je činí nadřazenými základním kalkulačkám. Zde je přehled těchto klíčových vlastností:

    • Základní aritmetika: Provádí standardní operace jako sčítání, odčítání, násobení a dělení, které jsou nezbytné pro každodenní výpočty.
    • Exponenciální funkce: Usnadňuje výpočty zahrnující mocniny a odmocniny, například čtverce a čtvercové odmocniny.
    • Trigonometrické funkce: Funkce jako sinus, kosinus a tangens (a jejich inverze) jsou klíčové pro řešení geometrických a fyzikálních problémů.
    • Logaritmické a exponenciální funkce: Vědecké kalkulačky zvládají výpočty s přirozenými (ln) a desítkovými logaritmy a také exponenciální výpočty.
    • Výpočty s komplexními čísly: Pro pokročilejší studia dokážou tyto kalkulačky provádět výpočty s komplexními čísly, nezbytné v inženýrství a fyzice.
    • Statistické funkce: Funkce pro výpočet průměru, směrodatné odchylky a dalších statistických hodnot jsou zahrnuty, což usnadňuje práci studentům i profesionálům.
    • Paměťové funkce: Hodnoty lze uložit a vyvolat, což zjednodušuje práci s vícekrokovými problémy.

    Vědecká kalkulačka online 991 Plus tyto schopnosti rozšiřuje o další funkce, jako jsou maticové výpočty, integrace, diferenciace a řešení rovnic, což z ní činí komplexní nástroj pro složité matematické úlohy.

    Skutečná vědecká kalkulačka

    3. Pochopení vědecké kalkulačky 991 Plus

    Vědecká kalkulačka 991 Plus je pokročilý nástroj používaný studenty a profesionály po celém světě. Klíčové prvky a funkce zahrnují:

    • Uživatelské rozhraní: Navrženo intuitivně, umožňuje uživatelům snadno zvládat složité operace.
    • Pokročilé matematické funkce: Podporuje další funkce jako hyperbolická trigonometrii, vektorové výpočty a statistickou regresi, ideální pro pokročilé studium a profesní úlohy.

    Její všestrannost a schopnost zvládat složité operace ji činí nejlepší volbou pro každého, kdo se zabývá intenzivními výpočty.

    4. Výhody používání online vědecké kalkulačky

    Naše online vědecká kalkulačka nabízí několik výhod oproti tradičním kalkulačkám:

    • Přístupnost: Přístupná kdykoliv a odkudkoliv prostřednictvím naší webové stránky, zajišťuje uživatelům dostupnost nezbytných matematických nástrojů kdekoliv jsou.
    • Nákladová efektivnost: Naše online verze je zdarma, čímž vám šetří náklady na nákup samostatného zařízení.
    • Kompatibilita zařízení: Ať už pracujete na stolním počítači, mobilu nebo tabletu, naše online kalkulačka je navržena tak, aby bez problémů fungovala na všech platformách.
    • Pravidelné aktualizace: S online platformou mohou být pravidelně přidávány nové funkce nebo aktualizace, což zajišťuje, že máte vždy přístup k nejnovějším nástrojům a opravám chyb.

    Navíc Vědecká kalkulačka online 991 Plus nabízí intuitivní uživatelské rozhraní, které uživatelům usnadňuje přechod z fyzické kalkulačky na online verzi bez ztráty produktivity.

    Online vědecká kalkulačka

    5. Aplikace vědecké kalkulačky

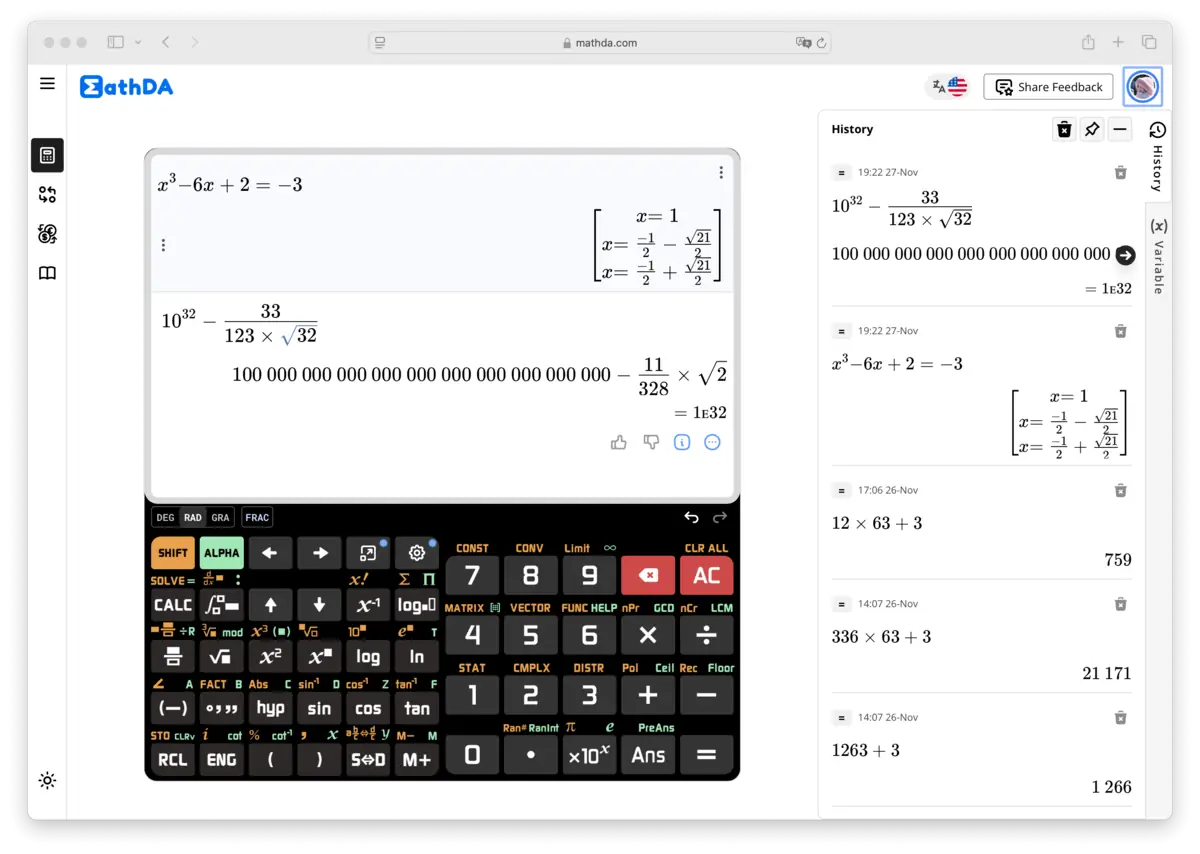
    Vědecké kalkulačky mají širokou škálu aplikací:

    • Vzdělání: Jsou nezbytné pro studenty STEM, pomáhají v předmětech od algebry po fyziku. Pokročilé funkce Vědecké kalkulačky online 991 Plus jsou obzvláště přínosné pro vyšší vzdělání, kde je vyžadováno řešení složitých problémů.
    • Profesionální využití: V inženýrství, fyzice a statistické analýze umožňují vědecké kalkulačky řešení složitých problémů, které jsou vyžadovány v mnoha technických oborech. Pokročilé funkce modelu 991 Plus ještě více podporují tyto profesní potřeby.
    • Každodenní použití: Vědecké kalkulačky lze použít pro každodenní výpočty jako jsou úroky z úvěru nebo konverze měn, což je činí užitečnými i mimo akademické a profesní prostředí.

    Flexibilita provádět tyto úkoly online zajišťuje, že uživatelé nikdy nebudou bez svých nezbytných výpočetních nástrojů, čímž šetří čas a úsilí.

    6. Tipy pro maximalizaci použití Vědecké kalkulačky online 991 Plus

    Pro co nejlepší využití Vědecké kalkulačky online 991 Plus zvažte následující:

    • Seznamte se s rozhraním: Věnujte čas, abyste se seznámili se všemi dostupnými funkcemi a zkratkami pro zlepšení efektivity výpočtů.
    • Pravidelná praxe: Používejte kalkulačku pravidelně, abyste se stali zběhlými v jejím používání pro různé úkoly.
    • Využijte online zdroje: Přistupujte k tutoriálům a průvodcům, které vysvětlují, jak provádět specifické výpočty, zejména složité funkce jako maticové operace nebo integrace.

    7. Závěr

    Naše online vědecká kalkulačka je výkonný a všestranný nástroj, který přenáší schopnosti fyzické vědecké kalkulačky do pohodlí vašeho prohlížeče. Ať už jste student, inženýr, nebo jen někdo, kdo potřebuje přesné výpočty, vybízíme vás, abyste ji vyzkoušeli.

    Vědecká kalkulačka online 991 Plus nabízí ještě více pokročilých funkcí, které splňují přísné požadavky akademických a profesních prostředí. Díky dostupnosti, cenové dostupnosti a všestrannosti naší online kalkulačky není potřeba investovat do fyzického zařízení. Prozkoumejte tento nástroj spolu s ostatními zdroji dostupnými na naší webové stránce a zjistěte, jak může náš vědecký kalkulátor podpořit vaše vzdělávací a profesní cíle.

    Často kladené otázky (FAQ) ohledně online vědeckých kalkulaček

    1. Co je online vědecká kalkulačka?

    Online vědecká kalkulačka je webový nástroj, který umožňuje uživatelům provádět složité matematické výpočty jako trigonometrii, logaritmy, exponenty, statistiky a další. Typicky napodobuje funkčnost fyzických vědeckých kalkulaček.

    2. Jak přistupuji k online vědecké kalkulačce?

    K online vědecké kalkulačce můžete přistupovat prostřednictvím různých webů nebo aplikací. Jednoduše vyhledejte "MatematikaDA online vědecká kalkulačka" ve vašem webovém prohlížeči a vyberte si tu, která nejlépe vyhovuje vašim potřebám.

    3. Musím stahovat nebo instalovat software, abych ji mohl používat?

    Ne, online vědecké kalkulačky fungují přímo v prohlížeči bez nutnosti stahování nebo instalace.

    4. Jaké typy výpočtů mohu provádět?

    Můžete provádět širokou škálu výpočtů, včetně:

    • Základní aritmetiky (sčítání, odčítání, násobení, dělení)
    • Trigonometrických funkcí (sin, cos, tan atd.)
    • Logaritmických a exponenciálních výpočtů
    • Statistických funkcí (průměr, směrodatná odchylka, regrese atd.)
    • Komplexních čísel a maticových operací
    • Jednotkových převodů

    5. Je to zdarma k použití?

    Naše online vědecká kalkulačka je zdarma k použití.

    6. Mohu grafovat funkce pomocí online vědecké kalkulačky?

    Ano, naše online vědecké kalkulačky obsahují funkce pro grafování. Můžete kreslit grafy pro lepší porozumění.

    7. Je online vědecká kalkulačka přesná?

    Ano, naše online kalkulačky jsou vysoce přesné.

    8. Mohu ji používat na svém smartphonu nebo tabletu?

    Ano, naše online vědecká kalkulačka je obvykle mobilně příjemná a dobře funguje na chytrých telefonech a tabletech.

    9. Jsou online vědecké kalkulačky bezpečné?

    Ano, naše online vědecká kalkulačka je bezpečná k použití.

    10. Může řešit rovnice nebo zobrazovat řešení krok za krokem?

    Ano, naše online kalkulačka může řešit rovnice.

    11. Existují nějaká omezení při používání online vědeckých kalkulaček?

    Naše online vědecká kalkulačka je mocná.

    12. Mohou ji studenti používat během zkoušek?

    To závisí na pravidlech zkoušky. Některé zkoušky umožňují použití online nástrojů, zatímco jiné je omezují, aby se zabránilo podvádění.

    13. Funguje naše online vědecká kalkulačka jako skutečná kalkulačka?

    Ano, naše online vědecká kalkulačka funguje jako skutečné vědecké kalkulačky, replikující chování fyzických kalkulaček.

    Formát výsledku
      • Vědecká konstanta
      • 1
        Proton mass
        1.67262189821e-27
        kg
        mp
      • 2
        Neutron mass
        1.67492747121e-27
        kg
        mn
      • 3
        Electron mass
        9.1093835611e-31
        kg
        me
      • 4
        Muon mass
        1.88353159448e-28
        kg
        mµ
      • 5
        Bohr radius
        5.291772106712e-11
        m
        a₀
      • 6
        Planck constant
        6.62607004081e-34
        Js
        h
      • 7
        Nuclear magneton
        5.05078369931e-27
        JT-1
        µN
      • 8
        Bohr magneton
        9.27400999457e-24
        JT-1
        µB
      • 9
        Planck constant,rationalized
        1.05457180013e-34
        Js
        ℏ
      • 10
        Fine-structure constant
        0.007297352566417
        α
      • 11
        Classical electron radius
        2.817940322719e-15
        m
        re
      • 12
        Compton wavelength
        2.426310236711e-12
        m
        λc
      • 13
        Proton gyromagnetic ratio
        267522190.018
        s-1T-1
        γp
      • 14
        Proton Compton wavelength
        1.3214098539661e-15
        m
        λcp
      • 15
        Neutron Compton wavelength
        1.3195909048188e-15
        m
        λcn
      • 16
        Rydberg constant
        10973731.56850865
        m-1
        R∞
      • 17
        Atomic mass constant
        1.6605390402e-27
        kg
        u
      • 18
        Proton magnetic moment
        1.410606787397e-26
        JT-1
        µp
      • 19
        Electron magnetic moment
        -9.28476462057e-24
        JT-1
        µe
      • 20
        Neutron magnetic moment
        -9.662365023e-27
        JT-1
        µn
      • 21
        Muon magnetic moment
        -4.490448261e-26
        JT-1
        µµ
      • 22
        Faraday constant
        96485.332895
        Cmol-1
        F
      • 23
        Elementary charge
        1.602176620898e-19
        C
        e
      • 24
        Avogadro constant
        6.02214085774e+23
        mol-1
        NA
      • 25
        Boltzmann constant
        1.3806485279e-23
        JK-1
        k
      • 26
        Molar volume of ideal
        0.02271094713
        m3mol-1
        Vm
      • 27
        Molar gas constant
        8.3144598484848
        Jmol-1K-1
        R
      • 28
        Speed of light in vacuum
        299792458
        ms-1
        C₀
      • 29
        First radiation constant
        3.74177179046e-16
        Wm2
        C₁
      • 30
        Second radiation constant
        0.014387773683
        mK
        C₂
      • 31
        Stefan-Boltzmann constant
        5.67036713e-8
        Wm-2K-4
        σ
      • 32
        Electric constant
        8.854187817e-12
        Fm-1
        ε₀
      • 33
        Magnetic constant
        0.00000125663706
        NA-2
        µ₀
      • 34
        Magnetic flux quantum
        2.06783383113e-15
        Wb
        φ₀
      • 35
        Standard acceleration of gravity
        9.80665
        ms-2
        g
      • 36
        Conductance quantum
        0.00007748091731018
        S
        G₀
      • 37
        Characteristic impedance of vacuum
        376.730313461
        Ω
        Z₀
      • 38
        Celsius temperature
        273.15
        K
        t
      • 39
        Newtonian constant of gravitation
        6.6740831e-11
        m3kg-1s-2
        G
      • 40
        Standard atmosphere
        101325
        Pa
        atm
      Metrycké konverze
      • 1
        in→cm
        inch (in) ► centimeter (cm)
      • 2
        cm→in
        centimeters to inches
      • 3
        ft→m
        foot (ft) ► meter (m)
      • 4
        m→ft
        meters to feet
      • 5
        yd→m
        yard (yd) ► meter (m)
      • 6
        m→yd
        meters to yards
      • 7
        mile→km
        mile (mi) ► kilometer (km)
      • 8
        km→mile
        kilometers to miles
      • 9
        n mile→m
      • 10
        m→n mile
      • 11
        acre→m²
        acre (based on U.S. survey foot)► square meter (m²)
      • 12
        m²→acre
        square meters to acres
      • 13
        gal(US)→L
        gallon (U.S.) (gal) ► liter (L)
      • 14
        L→gal(US)
        liters to US gallons
      • 15
        gal(UK)→L
        gallon [Canadian and U.K. (Imperial)] (gal) ► liter (L)
      • 16
        L→gal(UK)
        Liters to UK gallons
      • 17
        pc→km
        parsec (pc) ► meter (m)
      • 18
        km→pc
      • 19
        km/h→m/s
        kilometer per hour (km / h) ► meter per second (m / s)
      • 20
        m/s→km/h
        meters/second to kilometers/hour
      • 21
        oz→g
        ounce (avoirdupois) (oz) ► gram (g)
      • 22
        g→oz
        grams to ounces
      • 23
        lb→kg
        pound (troy or apothecary) (lb) ► kilogram (kg)
      • 24
        kg→lb
        kilograms to pounds
      • 25
        atm→Pa
        atmosphere, standard (atm) ► pascal (Pa)
      • 26
        Pa→atm
        Pascals to atmospheres
      • 27
        mmHg→Pa
        millimeter of mercury, conventional (mmHg) ► pascal (Pa)
      • 28
        Pa→mmHg
        Pascals to millimeters of mercury
      • 29
        hp→kW
        horsepower (550 ft · lbf / s) (hp) ► kilowatt (kW)
      • 30
        kW→hp
        kilowatt (kW) ► horsepower (550 ft · lbf / s) (hp)
      • 31
        kgf/cm²→Pa
        kilogram-force per square centimeter(kgf/cm2)) ► pascal (Pa)
      • 32
        Pa→kgf/cm²
      • 33
        kgf•m→J
      • 34
        J→kgf•m
      • 35
        lbf/in²→kPa
        pound-force per square inch (psi) (lbf/in2) ► pascal (Pa)
      • 36
        kPa→lbf/in²
      • 37
        °F→°C
        degree Fahrenheit (temperature) (ºF) ................... degree Celsius (ºC)
      • 38
        °C→°F
        Celsius to Farenheit
      • 39
        J→cal
        joule (J) ► calorieIT (calIT)
      • 40
        cal→J
        calorieIT (calIT) ► joule (J)
      Hyperbolic
      • 1
        Sinh(value)
        Hyperbolic sine
      • 2
        Cosh(value)
        Hyperbolic cosine
      • 3
        Tanh(value)
        Hyperbolic tangent
      • 4
        Coth(value)
        Hyperbolic cotangent
      • 5
        Sech(value)
        Hyperbolic secant
      • 6
        Csch(value)
        Hyperbolic cosecant
      • 7
        ArcSinh(value)
        Hyperbolic arcsine
      • 8
        ArcCosh(value)
        Hyperbolic arccosine
      • 9
        ArcTanh(value)
        Hyperbolic arctangent
      • 10
        ArcCoth(value)
        Inverse hyperbolic cotangent
      • 11
        ArcSech(value)
        Inverse hyperbolic secant
      • 12
        ArcCsch(value)
        Inverse hyperbolic cosecant
        • Additional trigonometric functions
      • 13
        Cot(expr)
        the cotangent function
      • 14
        ArcCot(z)
        returns the inverse cotangent of z
      • 15
        Sec(z)
        returns the secant of z
      • 16
        ArcSec(z)
        returns the inverse secant of z
      • 17
        Csc(z)
        returns the cosecant of z
      • 18
        ArcCsc(z)
        returns the inverse cosecant of z
      COMPLEX
      • 1
        Arg
        Argument of the complex number
      • 2
        Conjugate
        Conjugate of the complex number
      • 3
        Re
        Real component
      • 4
        Im
        Imaginary component
      • 5
        ▸r∠φ
        Displays the result in polar form
      • 6
        ▸a+bi
        Displays the result in rectangular form
      • 7
        Abs
        Returns the magnitude (modulus)
      Nastavení
      Potvrzení obnovení nastavení
      Tímto krokem trvale odstraníte vaše nastavení a obnovíte výchozí
      Formát desetinného čísla
      Matice
      • 1
        Vložit matici
      • 2
        Det(matrix)
        Calculates the determinant
      • 3
        Inverse(matrix)
        Compute the inverse of the matrix
      • 4
        MatrixRank(matrix)
        returns the rank of matrix
      • 5
        Transpose(matrix)
        Transposes the matrix
      • 6
        IdentityMatrix(dimension)
        Returns the identity matrix
      • 7
        RowReduce(matrix)
        Return the reduced row-echelon form
      • 8
        CharacteristicPolynomial(matrix, var)
        Computes the characteristic polynomial of a matrix for the variable var
      • 9
        Diagonal(list)
        Computes the diagonal vector of the matrix
      • 10
        DiagonalMatrix(list)
        Gives a matrix with the values in list on its diagonal and zeroes elsewhere
      • 11
        Eigenvalues(matrix)
        Get the numerical eigenvalues of the matrix
      • 12
        Eigenvectors(matrix)
        Get the numerical eigenvectors of the matrix
      • 13
        LeastSquares(matrix, right)
        Solves the linear least-squares problem 'matrix.x = right'
      • 14
        LinearSolve(matrix, right)
        Solves the linear equation system 'matrix.x = right' and returns one corresponding solution x
      • 15
        LUDecomposition(matrix)
        Calculate the LUP-decomposition of a square matrix
      • 16
        NullSpace(matrix)
        Returns a list of vectors that span the nullspace of the matrix
      • 17
        PseudoInverse(matrix)
        Computes the Moore-Penrose pseudoinverse of the matrix. If matrix is invertible, the pseudoinverse equals the inverse
      • 18
        SingularValueDecomposition(matrix)
        Calculates the singular value decomposition for the matrix
      Vložit matici
      Rozměry matice
      ✖
      1
      2
      3
      4
      5
      6
      7
      1
      2
      3
      4
      5
      6
      7
      Změnit rozvržení kalkulačky
      Který symbol by měla klávesa , reprezentovat?
      * Nastavení můžete později změnit v nastavení
      Přihlaste se, abyste využili všech funkcí
      • Historie výpočtů
      • Uložit a synchronizovat nastavení
      • Využívat pokročilé funkce
      Zpětná vazba k výpočtu
      Poskytnutí vašeho e-mailu nám pomůže efektivněji řešit váš problém (volitelné)