Der ultimative Leitfaden zu wissenschaftlichen Taschenrechnern

1. Einführung

Ein wissenschaftlicher Taschenrechner ist ein leistungsstarkes Werkzeug, das für komplexe mathematische Berechnungen ausgelegt ist, die über die Fähigkeiten eines Standardrechners hinausgehen. Er führt nicht nur grundlegende Rechenoperationen aus, sondern auch fortgeschrittene Funktionen, die für die höhere Bildung, Ingenieurwissenschaft, Naturwissenschaft und Mathematik unerlässlich sind. Wissenschaftliche Taschenrechner sind in Bildungs- und Berufsumgebungen von unschätzbarem Wert und unterstützen Studierende und Fachleute bei präzisen Berechnungen.

Ergänzend zu physischen Taschenrechnern gibt es einen praktischen Online-Wissenschaftlichen Taschenrechner auf unserer Website. Dieses Tool spiegelt die Funktionen traditioneller wissenschaftlicher Taschenrechner wider und bietet zudem den Vorteil, von jedem internetfähigen Gerät aus zugänglich zu sein, sodass Berechnungen immer in Reichweite sind. Der Wissenschaftliche Taschenrechner Online 991 Plus ist eine erweiterte Version mit einer Vielzahl von Funktionen für komplexe mathematische Operationen, die den Anforderungen von Studierenden, Lehrenden und Fachleuten gerecht wird.

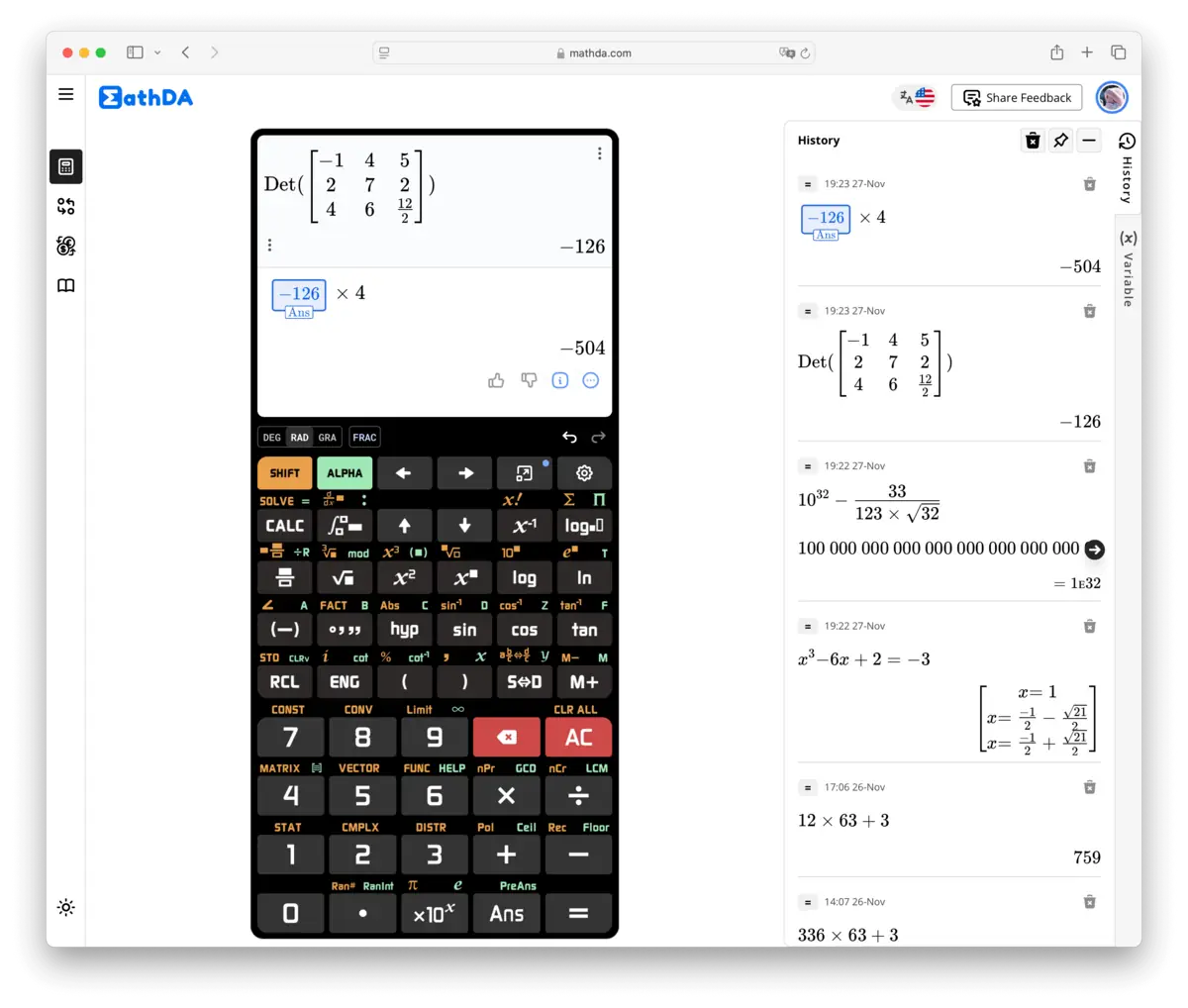
2. Wichtige Funktionen eines wissenschaftlichen Taschenrechners

Wissenschaftliche Taschenrechner sind mit einer Vielzahl von Funktionen ausgestattet, die sie gegenüber einfachen Rechnern überlegen machen. Hier eine Übersicht dieser Schlüsselmerkmale:

• Grundrechenarten: Führen Standardoperationen wie Addition, Subtraktion, Multiplikation und Division aus, die für alltägliche Berechnungen notwendig sind.
• Exponentialfunktionen: Berechnungen, die Exponenten und Wurzeln beinhalten, werden einfach gemacht. Dazu gehören Quadrate, Quadratwurzeln und andere Potenzen.
• Trigonometrische Funktionen: Funktionen wie Sinus, Kosinus und Tangens (sowie deren Umkehrungen) sind entscheidend für die Lösung von Geometrie- und Physikproblemen.
• Logarithmische und Exponentialfunktionen: Wissenschaftliche Rechner behandeln sowohl natürliche (ln) als auch dekadische Logarithmen sowie Exponentialoperationen.
• Berechnungen mit komplexen Zahlen: Für fortgeschrittene Studien können diese Rechner Berechnungen mit komplexen Zahlen durchführen, die in Ingenieurwissenschaften und Physik unerlässlich sind.
• Statistische Funktionen: Funktionen zur Berechnung von Mittelwert, Standardabweichung und anderen statistischen Werten sind enthalten, was es Studierenden und Fachleuten gleichermaßen erleichtert.
• Speicherfunktionen: Werte können gespeichert und abgerufen werden, was den Prozess bei der Arbeit mit mehrstufigen Problemen vereinfacht.

Der Wissenschaftliche Taschenrechner Online 991 Plus verbessert diese Fähigkeiten und bietet zusätzliche Funktionen wie Matrizenberechnungen, Integration, Differentiation und Gleichungslösungen, wodurch er ein umfassendes Werkzeug für komplexe mathematische Aufgaben darstellt.

3. Verständnis des Wissenschaftlichen Taschenrechners 991 Plus

Der Wissenschaftliche Taschenrechner 991 Plus ist ein fortschrittliches Werkzeug, das von Studierenden und Fachleuten weltweit genutzt wird. Wichtige Komponenten und Merkmale umfassen:

• Benutzeroberfläche: Entwickelt, um intuitiv zu sein, ermöglicht sie es Nutzern, komplexe Operationen einfach zu navigieren.
• Erweiterte mathematische Funktionen: Unterstützt zusätzliche Funktionen wie hyperbolische Trigonometrie, Vektorrechnungen und statistische Regression, ideal für fortgeschrittene Studien und berufliche Aufgaben.

Seine Vielseitigkeit und seine Fähigkeit, komplexe Operationen zu bewältigen, machen ihn zur ersten Wahl für alle, die intensive Berechnungen durchführen müssen.

4. Vorteile der Nutzung eines Online-Wissenschaftlichen Taschenrechners

Unser Online-Wissenschaftlicher Taschenrechner bietet mehrere Vorteile gegenüber herkömmlichen Rechnern:

• Zugänglichkeit: Jederzeit und überall über unsere Website zugänglich, stellt er sicher, dass Nutzer immer über wesentliche mathematische Werkzeuge verfügen.
• Kosteneffizienz: Im Gegensatz zu einem physischen Rechner ist unsere Online-Version kostenlos nutzbar, was Ihnen die Anschaffung eines separaten Geräts erspart.
• Gerätekompatibilität: Egal, ob Sie am Desktop, mobil oder am Tablet arbeiten, unser Online-Rechner ist so konzipiert, dass er nahtlos auf allen Plattformen funktioniert.
• Regelmäßige Updates: Mit einer Online-Plattform können neue Funktionen oder Updates regelmäßig hinzugefügt werden, sodass Sie immer Zugriff auf die neuesten Werkzeuge und Fehlerbehebungen haben.

Zusätzlich bietet der Wissenschaftliche Taschenrechner Online 991 Plus eine intuitive Benutzeroberfläche, die es den Nutzern erleichtert, den Übergang von einem physischen Rechner zu einer Online-Version ohne Produktivitätsverlust zu vollziehen.

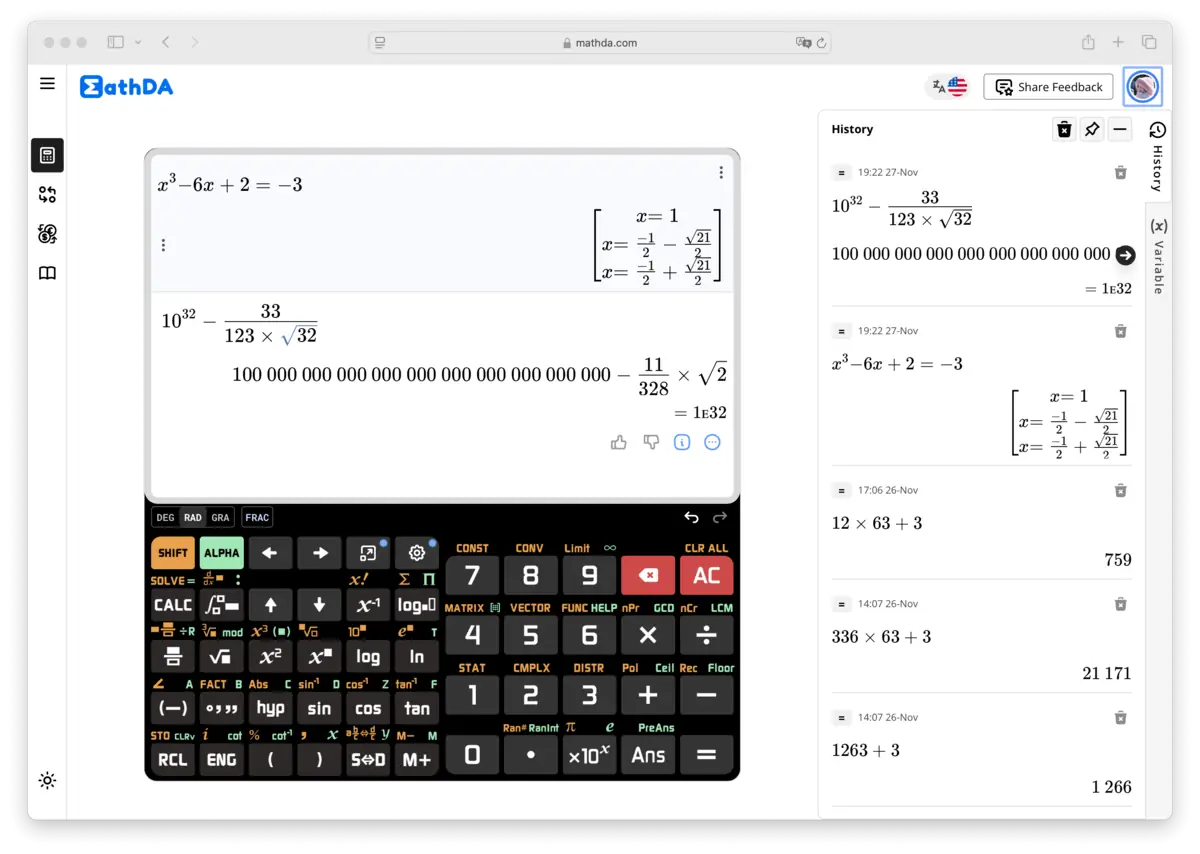
5. Anwendungen eines wissenschaftlichen Taschenrechners

Wissenschaftliche Taschenrechner haben ein breites Anwendungsspektrum:

• Bildung: Sie sind für MINT-Studenten unverzichtbar und unterstützen Fächer von Algebra bis Physik. Die erweiterten Funktionen des Wissenschaftlichen Taschenrechners Online 991 Plus sind besonders für die höhere Bildung von Vorteil, bei der komplexe Problemlösungen erforderlich sind.
• Berufliche Nutzung: In Ingenieurwissenschaften, Physik und statistischer Analyse ermöglichen wissenschaftliche Taschenrechner komplexe Problemlösungen, die in vielen technischen Bereichen erforderlich sind. Die erweiterten Funktionen des Modells 991 Plus unterstützen diese beruflichen Bedürfnisse weiter.
• Alltagsgebrauch: Wissenschaftliche Taschenrechner können für Haus- und Finanzberechnungen genutzt werden, wie z.B. die Berechnung von Kreditinteressen oder Währungsumrechnungen, was sie auch außerhalb von akademischen und beruflichen Umgebungen nützlich macht.

Die Möglichkeit, diese Aufgaben online zu erledigen, stellt sicher, dass Nutzer niemals ohne ihre wesentlichen Rechenwerkzeuge sind, was Zeit und Mühe spart.

6. Tipps zur optimalen Nutzung des wissenschaftlichen Taschenrechners Online 991 Plus

Um das Beste aus dem Wissenschaftlichen Taschenrechner Online 991 Plus herauszuholen, sollten Sie folgende Punkte beachten:

• Machen Sie sich mit der Benutzeroberfläche vertraut: Nehmen Sie sich Zeit, um alle verfügbaren Funktionen und Tastenkombinationen kennenzulernen, um die Effizienz bei Berechnungen zu verbessern.
• Regelmäßige Übung: Nutzen Sie den Taschenrechner regelmäßig, um die Fähigkeiten zu meistern, ihn für verschiedene Aufgaben effektiv zu verwenden.
• Nutzen Sie Online-Ressourcen: Greifen Sie auf Tutorials und Anleitungen zu, die erklären, wie spezifische Berechnungen durchgeführt werden, insbesondere komplexe Funktionen wie Matrizenoperationen oder Integration.

7. Fazit

Unser Online-Wissenschaftlicher Taschenrechner ist ein leistungsstarkes und vielseitiges Werkzeug, das die Fähigkeiten eines physischen wissenschaftlichen Taschenrechners mit der Bequemlichkeit Ihres Browsers vereint. Egal ob Sie Studierender, Ingenieur oder einfach jemand sind, der präzise Berechnungen benötigt, wir laden Sie ein, es auszuprobieren.

Der Wissenschaftliche Taschenrechner Online 991 Plus bietet sogar noch weiter fortgeschrittene Funktionen, die den strengen Anforderungen in akademischen und beruflichen Umgebungen gerecht werden. Mit der Zugänglichkeit, Erschwinglichkeit und Vielseitigkeit unseres Online-Rechners gibt es keinen Grund, in ein physisches Gerät zu investieren. Entdecken Sie dieses Tool zusammen mit anderen Ressourcen auf unserer Website und sehen Sie, wie unser wissenschaftlicher Taschenrechner Ihre Bildungs- und Berufsziele unterstützen kann.

Häufig gestellte Fragen (FAQ) zu Online-Wissenschaftlichen Taschenrechnern

1. Was ist ein Online-Wissenschaftlicher Taschenrechner?

Ein Online-Wissenschaftlicher Taschenrechner ist ein webbasiertes Tool, das es Nutzern ermöglicht, komplexe mathematische Berechnungen wie Trigonometrie, Logarithmen, Potenzen, Statistik und mehr durchzuführen. Er ahmt in der Regel die Funktionalität physischer wissenschaftlicher Taschenrechner nach.

2. Wie greife ich auf einen Online-Wissenschaftlichen Taschenrechner zu?

Sie können über verschiedene Websites oder Apps auf einen Online-Wissenschaftlichen Taschenrechner zugreifen. Suchen Sie einfach in Ihrem Webbrowser nach "MathDA wissenschaftlicher Taschenrechner" und wählen Sie denjenigen, der Ihren Bedürfnissen entspricht.

3. Muss ich Software herunterladen oder installieren, um ihn zu benutzen?

Nein, Online-Wissenschaftliche Taschenrechner funktionieren direkt in Ihrem Browser, ohne dass Downloads oder Installationen erforderlich sind.

4. Welche Art von Berechnungen kann ich durchführen?

Sie können ein breites Spektrum an Berechnungen durchführen, darunter:

• Grundrechenarten (Addition, Subtraktion, Multiplikation, Division)
• Trigonometrische Funktionen (Sinus, Kosinus, Tangens, etc.)
• Logarithmische und exponentielle Berechnungen
• Statistische Funktionen (Mittelwert, Standardabweichung, Regression, etc.)
• Komplexe Zahlen und Matrizenoperationen
• Einheitenumrechnungen

5. Ist die Nutzung kostenlos?

Unser Online-Wissenschaftlicher Taschenrechner ist kostenlos nutzbar.

6. Kann ich mit einem Online-Wissenschaftlichen Taschenrechner Funktionen graphisch darstellen?

Ja, unsere Online-Wissenschaftlichen Taschenrechner beinhalten graphische Features. Sie können Funktionen darstellen, um ein besseres Verständnis zu bekommen.

7. Ist ein Online-Wissenschaftlicher Taschenrechner genau?

Ja, unsere Online-Rechner sind sehr genau.

8. Kann ich ihn auf meinem Smartphone oder Tablet verwenden?

Ja, unser Online-Wissenschaftlicher Taschenrechner ist in der Regel mobilfreundlich und funktioniert gut auf Smartphones und Tablets.

9. Sind Online-Wissenschaftliche Taschenrechner sicher?

Ja, unser Online-Wissenschaftlicher Taschenrechner ist sicher in der Nutzung.

10. Kann er Gleichungen lösen oder Schritt-für-Schritt-Lösungen anzeigen?

Ja, unser Online-Rechner kann Gleichungen lösen.

11. Gibt es Einschränkungen bei der Nutzung von Online-Wissenschaftlichen Taschenrechnern?

Unser Online-Wissenschaftlicher Taschenrechner ist leistungsstark.

12. Können Studierende sie während Prüfungen verwenden?

Das hängt von den Prüfungsregeln ab. Einige Prüfungen erlauben die Nutzung von Online-Tools, während andere sie einschränken, um Schummeln zu verhindern.

13. Funktioniert unser Online-Wissenschaftlicher Taschenrechner wie ein echter Taschenrechner?

Ja, unser Online-Wissenschaftlicher Taschenrechner funktioniert wie echte wissenschaftliche Taschenrechner und repliziert das Verhalten physischer Rechner.