Ο Απόλυτος Οδηγός για Επιστημονικές Αριθμομηχανές
1. Εισαγωγή
Μια επιστημονική αριθμομηχανή είναι ένα ισχυρό εργαλείο σχεδιασμένο για σύνθετους μαθηματικούς υπολογισμούς, ξεπερνώντας τις δυνατότητες μιας απλής αριθμομηχανής. Δεν περιορίζεται μόνο σε βασικές αριθμητικές πράξεις, αλλά επεκτείνεται σε πιο εξελιγμένες λειτουργίες που είναι απαραίτητες για την ανώτατη εκπαίδευση, την επιστήμη και τη μηχανική. Οι επιστημονικές αριθμομηχανές είναι ανεκτίμητες τόσο στον εκπαιδευτικό όσο και στον επαγγελματικό τομέα, υποστηρίζοντας μαθητές και επαγγελματίες με ακριβείς υπολογισμούς.

Εκτός από τις φυσικές αριθμομηχανές, υπάρχει μια βολική online επιστημονική αριθμομηχανή διαθέσιμη στην ιστοσελίδα μας. Αυτό το εργαλείο μιμείται τις λειτουργίες των παραδοσιακών επιστημονικών αριθμομηχανών και προσθέτει το πλεονέκτημα της πρόσβασης από οποιαδήποτε συσκευή με σύνδεση στο διαδίκτυο. Η Scientific Calculator Online 991 Plus είναι μια αναβαθμισμένη έκδοση που προσφέρει πληθώρα λειτουργιών, κατάλληλες για πολύπλοκες μαθηματικές πράξεις, εξυπηρετώντας τις ανάγκες μαθητών, εκπαιδευτικών και επαγγελματιών.
2. Κύρια Χαρακτηριστικά μιας Επιστημονικής Αριθμομηχανής
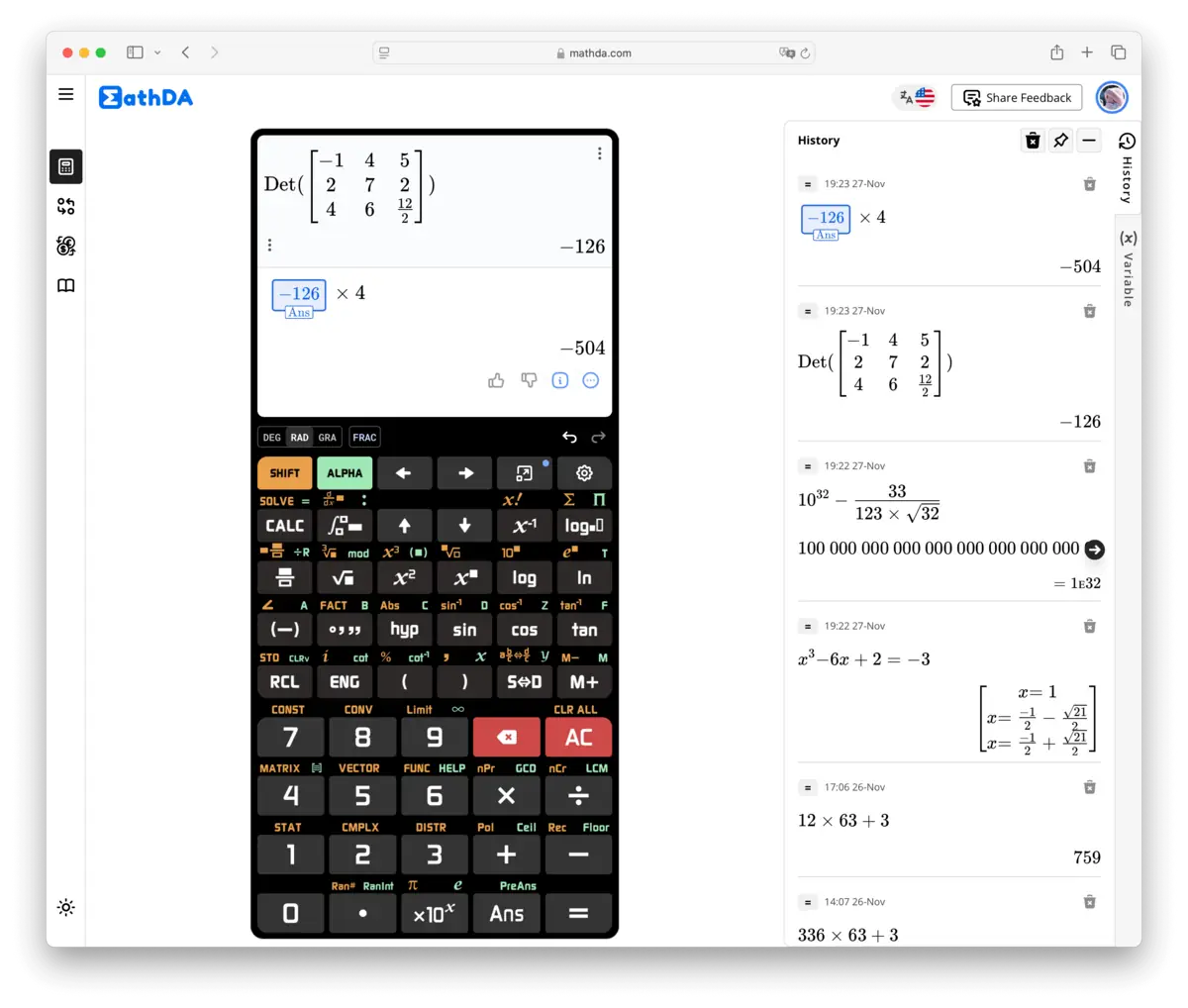
Οι επιστημονικές αριθμομηχανές είναι εξοπλισμένες με μια ποικιλία λειτουργιών που τις καθιστούν ανώτερες από τις απλές αριθμομηχανές. Ας δούμε αυτά τα κύρια χαρακτηριστικά:
- Βασική Αριθμητική: Εκτελεί βασικές πράξεις, όπως πρόσθεση, αφαίρεση, πολλαπλασιασμό και διαίρεση, απαραίτητες για καθημερινές υπολογιστικές ανάγκες.
- Εκθετικές Λειτουργίες: Διευκολύνει τους υπολογισμούς που αφορούν δυνάμεις και ρίζες, όπως τα τετράγωνα, οι τετραγωνικές ρίζες κλπ.
- Τριγωνομετρικές Λειτουργίες: Περιλαμβάνει συναρτήσεις όπως το ημίτονο, το συνημίτονο και την εφαπτομένη (και τις αντίστροφές τους), κρίσιμες για προβλήματα γεωμετρίας και φυσικής.
- Λογαριθμικές και Εκθετικές Λειτουργίες: Χειρίζεται τόσο τους φυσικούς (ln) όσο και τους λογαρίθμους βάσης-10, καθώς και εκθετικές πράξεις.
- Υπολογισμοί Σύνθετων Αριθμών: Για πιο προχωρημένες σπουδές, οι αριθμομηχανές αυτές μπορούν να διενεργούν υπολογισμούς με σύνθετους αριθμούς.
Η Scientific Calculator Online 991 Plus ενισχύει αυτές τις δυνατότητες, προσφέροντας πρόσθετες λειτουργίες, όπως υπολογισμούς πινάκων, ολοκλήρωσης, παραγώγισης και επίλυσης εξισώσεων, καθιστώντας την ένα ολοκληρωμένο εργαλείο για πολύπλοκες μαθηματικές εργασίες.

3. Κατανόηση της Scientific Calculator 991 Plus
Η Scientific Calculator 991 Plus είναι ένα προηγμένο εργαλείο που χρησιμοποιείται από μαθητές και επαγγελματίες παγκοσμίως. Τα κύρια χαρακτηριστικά της περιλαμβάνουν:
- Διεπαφή Χρήστη: Σχεδιασμένη για να είναι διαισθητική, επιτρέπει στους χρήστες να πλοηγούνται εύκολα σε πολύπλοκες λειτουργίες.
- Προηγμένες Μαθηματικές Λειτουργίες: Υποστηρίζει επιπλέον λειτουργίες όπως υπερβολική τριγωνομετρία, υπολογισμούς διανυσμάτων και στατιστική παλινδρόμηση.
Η ευελιξία της και η ικανότητά της να διαχειρίζεται περίπλοκες λειτουργίες την καθιστούν κορυφαία επιλογή για οποιονδήποτε ασχολείται με εντατικούς υπολογισμούς.
4. Πλεονεκτήματα Χρήσης μιας Online Επιστημονικής Αριθμομηχανής
Η online επιστημονική αριθμομηχανή μας προσφέρει πολλά οφέλη σε σχέση με τις παραδοσιακές αριθμομηχανές:
- Προσβασιμότητα: Είναι προσβάσιμη οποτεδήποτε και οπουδήποτε μέσω της ιστοσελίδας μας, εξασφαλίζοντας ότι οι χρήστες έχουν πάντα πρόσβαση σε βασικά μαθηματικά εργαλεία.
- Οικονομικότητα: Σε αντίθεση με μια φυσική αριθμομηχανή, η online εκδοχή μας είναι δωρεάν προς χρήση, εξοικονομώντας το κόστος αγοράς.
- Συμβατότητα Συσκευών: Είτε βρίσκεστε σε επιτραπέζιο υπολογιστή, κινητό ή tablet, η online αριθμομηχανή μας είναι σχεδιασμένη για να λειτουργεί άψογα σε όλες τις πλατφόρμες.
Επιπλέον, η Scientific Calculator Online 991 Plus προσφέρει διαισθητική διεπαφή χρήστη, καθιστώντας εύκολη τη μετάβαση από μια φυσική αριθμομηχανή σε μια online έκδοση χωρίς απώλεια παραγωγικότητας.
5. Εφαρμογές μιας Επιστημονικής Αριθμομηχανής
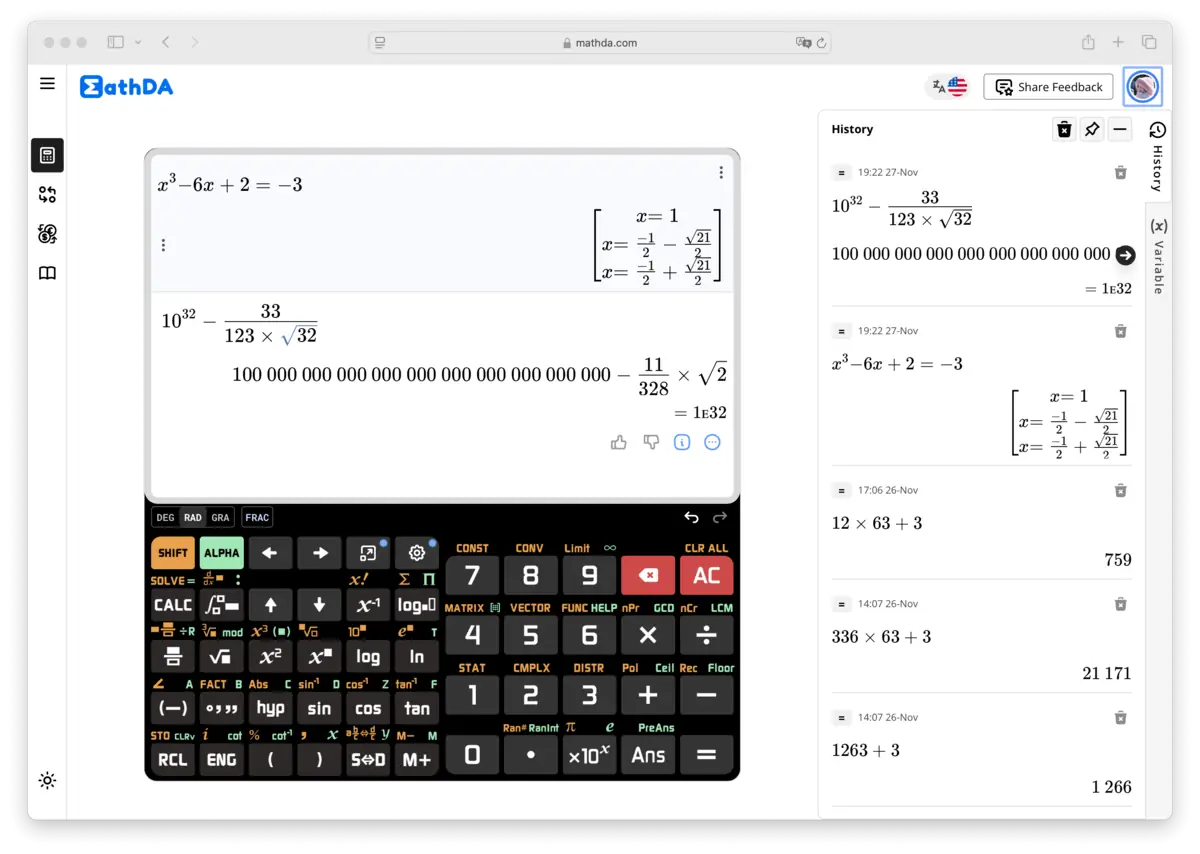
Οι επιστημονικές αριθμομηχανές εξυπηρετούν μια μεγάλη γκάμα εφαρμογών:
- Εκπαίδευση: Είναι απαραίτητες για μαθητές STEM, βοηθώντας σε μαθήματα από την άλγεβρα μέχρι τη φυσική.
- Επαγγελματική Χρήση: Στη μηχανική, τη φυσική και την στατιστική ανάλυση, οι επιστημονικές αριθμομηχανές επιτρέπουν επίλυση πολύπλοκων προβλημάτων που απαιτούνται σε πολλούς τεχνικούς τομείς.
Η ευελιξία να εκτελείτε αυτές τις εργασίες online εξασφαλίζει ότι οι χρήστες δεν μένουν ποτέ χωρίς τα απαραίτητα υπολογιστικά εργαλεία, εξοικονομώντας χρόνο και κόπο.
6. Συμβουλές για τη Μέγιστη Χρήση της Scientific Calculator Online 991 Plus
Για να αξιοποιήσετε πλήρως τη Scientific Calculator Online 991 Plus, εξετάστε τα εξής:
- Εξοικείωση με τη Διεπαφή: Αφιερώστε χρόνο για να γνωρίσετε όλες τις διαθέσιμες λειτουργίες και συντομεύσεις για βελτίωση της αποδοτικότητας.
- Συχνή Πρακτική: Χρησιμοποιείτε την αριθμομηχανή τακτικά για να εξοικειωθείτε με τη χρήση της σε ποικιλία εργασιών.
- Αξιοποίηση Διαδικτυακών Πόρων: Αξιοποιήστε σεμινάρια και οδηγούς που εξηγούν πώς να εκτελέσετε συγκεκριμένους υπολογισμούς, ειδικά σε πολύπλοκες λειτουργίες όπως οι πράξεις μήτρων ή η ολοκλήρωση.
7. Συμπέρασμα
Η online επιστημονική αριθμομηχανή μας είναι ένα ισχυρό και ευέλικτο εργαλείο που φέρνει τις δυνατότητες μιας φυσικής επιστημονικής αριθμομηχανής στην άνεση του προγράμματος περιήγησής σας. Είτε είστε μαθητής, μηχανικός ή απλώς κάποιος που χρειάζεται ακριβείς υπολογισμούς, σας ενθαρρύνουμε να τη δοκιμάσετε. Η Scientific Calculator Online 991 Plus προσφέρει ακόμα πιο προηγμένες λειτουργίες που ικανοποιούν τις απαιτητικές ανάγκες των ακαδημαϊκών και επαγγελματικών περιβαλλόντων. Με την προσβασιμότητα, την οικονομικότητα και την ευελιξία της online αριθμομηχανής μας, δεν υπάρχει λόγος να επενδύσετε σε φυσική συσκευή. Εξερευνήστε αυτό το εργαλείο μαζί με τους άλλους πόρους που διατίθενται στην ιστοσελίδα μας, και ανακαλύψτε πώς η επιστημονική αριθμομηχανή μας μπορεί να υποστηρίξει τους εκπαιδευτικούς και επαγγελματικούς σας στόχους.
Συχνές Ερωτήσεις (FAQ) για Online Επιστημονικές Αριθμομηχανές
1. Τι είναι μια online επιστημονική αριθμομηχανή;
Μια online επιστημονική αριθμομηχανή είναι ένα εργαλείο που βασίζεται στον ιστό και επιτρέπει στους χρήστες να εκτελούν σύνθετους μαθηματικούς υπολογισμούς όπως τριγωνομετρία, λογαριθμούς, εκθέτες, στατιστικά κ.λπ. Συνήθως μιμείται τη λειτουργικότητα των φυσικών επιστημονικών αριθμομηχανών.
2. Πώς μπορώ να αποκτήσω πρόσβαση σε μια online επιστημονική αριθμομηχανή;
Μπορείτε να αποκτήσετε πρόσβαση σε online επιστημονική αριθμομηχανή μέσω διάφορων ιστότοπων ή εφαρμογών. Απλά αναζητήστε "MathDA επιστημονική αριθμομηχανή" στον περιηγητή σας και επιλέξτε αυτή που ανταποκρίνεται στις ανάγκες σας.
3. Χρειάζεται να κατεβάσω ή να εγκαταστήσω κάποιο λογισμικό για τη χρήση της;
Όχι, οι online επιστημονικές αριθμομηχανές λειτουργούν απευθείας στον περιηγητή σας χωρίς να απαιτείται λήψη ή εγκατάσταση.
4. Τι είδους υπολογισμούς μπορώ να εκτελέσω;
Μπορείτε να εκτελέσετε ένα ευρύ φάσμα υπολογισμών, συμπεριλαμβανομένων:
- Βασικής αριθμητικής (πρόσθεση, αφαίρεση, πολλαπλασιασμός, διαίρεση)
- Τριγωνομετρικών συναρτήσεων (sin, cos, tan, κ.λπ.)
- Λογαριθμικών και εκθετικών υπολογισμών
- Στατιστικών λειτουργιών (μέση τιμή, τυπική απόκλιση, παλινδρόμηση, κ.λπ.)
- Σύνθετων αριθμών και πράξεων μήτρας
- Μετατροπών μονάδων
5. Είναι δωρεάν για χρήση;
Η online επιστημονική αριθμομηχανή μας είναι δωρεάν προς χρήση.
6. Μπορώ να σχεδιάσω γραφήματα χρησιμοποιώντας μια online επιστημονική αριθμομηχανή;
Ναι, οι online επιστημονικές αριθμομηχανές περιλαμβάνουν δυνατότητες γραφήματος. Μπορείτε να σχεδιάσετε συναρτήσεις για καλύτερη κατανόηση.
7. Είναι ακριβής μια online επιστημονική αριθμομηχανή;
Ναι, οι online αριθμομηχανές μας είναι ιδιαίτερα ακριβείς.
8. Μπορώ να τη χρησιμοποιήσω στο smartphone ή το tablet μου;
Ναι, η online επιστημονική αριθμομηχανή μας είναι συνήθως φιλική προς τις κινητές συσκευές και λειτουργεί καλά σε smartphones και tablets.
9. Είναι ασφαλείς οι online επιστημονικές αριθμομηχανές;
Ναι, η online επιστημονική αριθμομηχανή μας είναι ασφαλής στη χρήση.
10. Μπορεί να λύσει εξισώσεις ή να δείξει λύσεις βήμα προς βήμα;
Ναι, η online αριθμομηχανή μας μπορεί να λύσει εξισώσεις.
11. Υπάρχουν περιορισμοί στη χρήση online επιστημονικών αριθμομηχανών;
Η online επιστημονική αριθμομηχανή μας είναι ισχυρή.
12. Μπορούν οι μαθητές να τη χρησιμοποιούν κατά τη διάρκεια εξετάσεων;
Εξαρτάται από τους κανόνες των εξετάσεων. Ορισμένες εξετάσεις επιτρέπουν τη χρήση online εργαλείων, ενώ άλλες τις περιορίζουν για την αποφυγή αντιγραφής.
13. Η online επιστημονική αριθμομηχανή μας λειτουργεί όπως μια πραγματική αριθμομηχανή;
Ναι, η online επιστημονική αριθμομηχανή μας λειτουργεί όπως τις φυσικές επιστημονικές αριθμομηχανές, αναπαράγοντας τη συμπεριφορά των φυσικών αριθμομηχανών.