Galutinis vadovas apie mokslinius skaičiuotuvus

1. Įvadas

Mokslinis skaičiuotuvas yra galingas įrankis, skirtas sudėtingiems matematiniams skaičiavimams, kurie žymiai pranoksta standartinio skaičiuotuvo galimybes. Jis ne tik atlieka pagrindinius aritmetinius veiksmus, bet ir pažangias funkcijas, kurios būtinos aukštajam mokslui, inžinerijai, mokslams ir matematikai. Moksliniai skaičiuotuvai yra neįkainojami mokymo ir profesinėse srityse, padedantys studentams ir specialistams atlikti tikslius skaičiavimus.

Be fizinių skaičiuotuvų, mūsų svetainėje yra patogus mokslinio skaičiuotuvo internetinis variantas. Šis įrankis atkartoja tradicinių mokslinių skaičiuotuvų funkcijas ir prideda prieigą iš bet kokio prietaiso su interneto ryšiu, užtikrinant, kad skaičiavimai visada būtų po ranka. Mokslinis skaičiuotuvas online 991 Plus yra pažangi versija, siūlanti daug funkcijų, skirtų sudėtingiems matematiniams veiksmams, atitinkančioms studentų, mokytojų ir profesionalų poreikius.

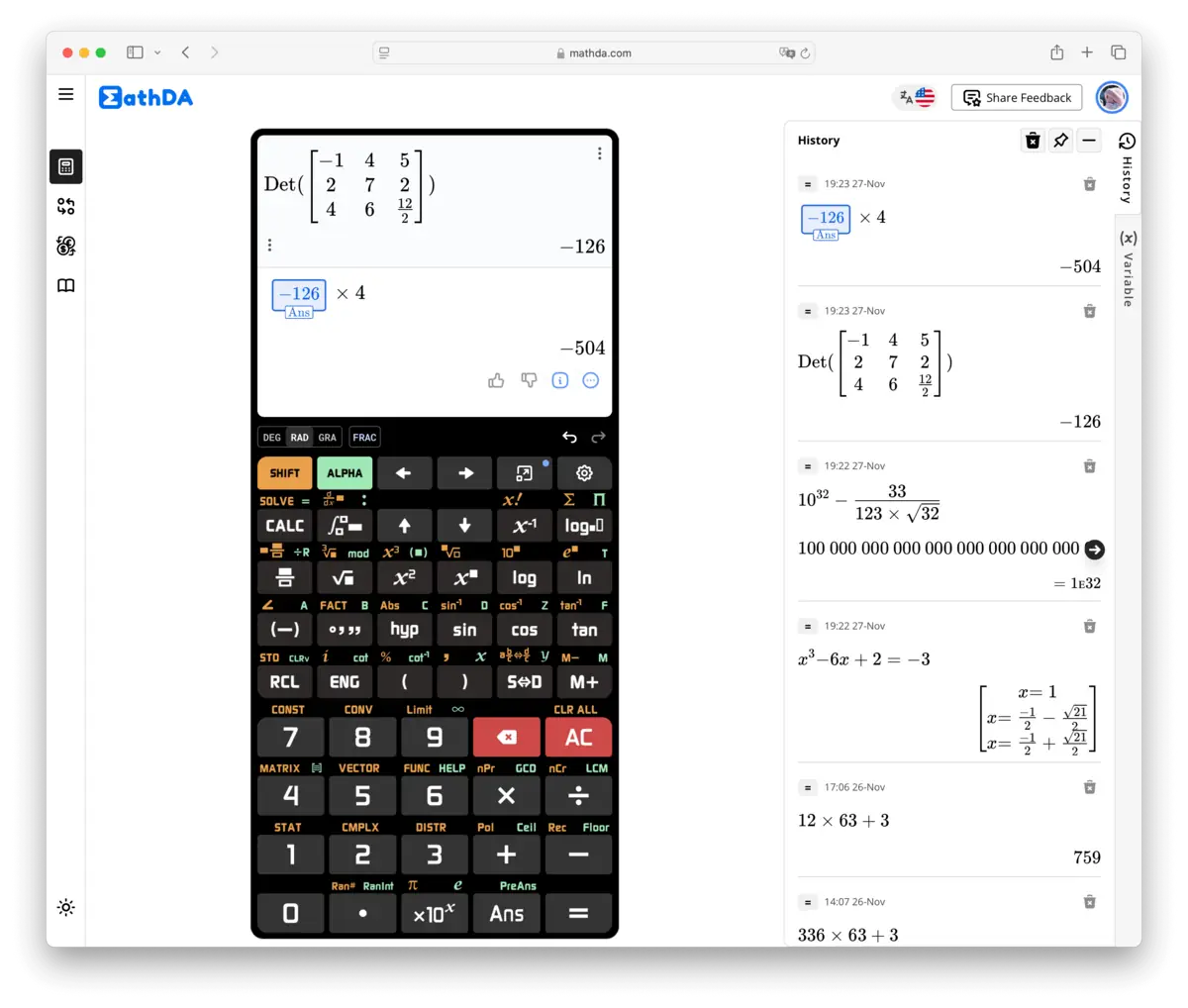
2. Mokslinio skaičiuotuvo ypatybės

Moksliniai skaičiuotuvai yra pilni įvairių funkcijų, dėl kurių jie yra pranašesni už pagrindinius skaičiuotuvus. Štai pagrindinės funkcijos:

• Pagrindinė Aritmetika: Atlieka standartinius veiksmus, tokius kaip sudėtis, atimtis, daugyba ir dalyba, kurie būtini kasdieniams skaičiavimams.
• Eksponentinės Funkcijos: Lengva atlikti skaičiavimus su laipsniais ir šaknimis, įskaitant kvadratus, kvadratines šaknis ir kitas potencias.
• Trigonometrijos Funkcijos: Funkcijos, tokios kaip sinusas, kosinusas ir tangentė (ir jų atvirkštiniai), yra būtinos geometrijos ir fizikos problemų sprendimui.
• Logaritminės ir Eksponentinės Funkcijos: Moksliniai skaičiuotuvai palaiko tiek natūralius (ln), tiek dešimtainius logaritmus, taip pat eksponentinius veiksmus.
• Sudėtingų Skaičių Skaičiavimai: Sudėtingesnių studijų metu šie skaičiuotuvai gali atlikti skaičiavimus su kompleksiniais skaičiais, būtinais inžinerijoje ir fizikoje.
• Statistinės Funkcijos: Yra galimybė skaičiuoti vidurkį, standartinį nuokrypį ir kitus statistinius rodiklius, palengvinanti studentų ir profesionalų darbą.
• Atminties Funkcijos: Suteikia galimybę saugoti ir atkurti vertes, kas palengvina daugiapakopių problemų sprendimą.

Mokslinis skaičiuotuvas online 991 Plus patobulina šias galimybes, siūlydamas papildomas funkcijas, tokias kaip matricų skaičiavimai, integravimas, diferencijavimas ir lygčių sprendimas, padarant jį visapusišku įrankiu sudėtingiems matematikos uždaviniams.

3. Suprasdami Mokslinį Skaičiuotuvą 991 Plus

Mokslinis skaičiuotuvas 991 Plus yra pažangus įrankis, naudojamas studentų ir profesionalų visame pasaulyje. Pagrindinės dalys ir funkcijos:

• Vartotojo Sąsaja: Sukurta taip, kad būtų intuityvi, leidžianti lengvai naviguoti per sudėtingus veiksmus.
• Pažangios Matematines Funkcijos: Palaiko papildomas funkcijas, tokias kaip hiperbolinės trigonometrijos, vektorių skaičiavimai ir statistinė regresija, idealiai tinkančios pažangioms studijoms ir profesiniams užduotims.

Jo universalumas ir gebėjimas atlikti sudėtingus veiksmus daro jį geriausiu pasirinkimu bet kam, kas turi reikalų su intensyviais skaičiavimais.

4. Privalumai naudojant Internetinį Mokslinį Skaičiuotuvą

Mūsų internetinis mokslinis skaičiuotuvas siūlo keletą privalumų prieš tradicinius skaičiuotuvus:

• Prieinamumas: Prieinamas bet kada ir bet kur mūsų svetainėje, užtikrina, kad vartotojai turėtų prieigą prie esminių matematinių įrankių, kur tik jie bebūtų.
• Ekonomija: Skirtingai nuo fizinio skaičiuotuvo, mūsų internetinė versija yra nemokama, taupanti jūsų pinigus, kuriuos reikėtų skirti atskiro įrenginio pirkimui.
• Įrenginių Suderinamumas: Nesvarbu, ar naudojate stalini kompiuterį, mobilųjį telefoną ar planšetę, mūsų internetinis skaičiuotuvas yra sukurtas, kad veiktų sklandžiai visose platformose.
• Reguliarūs Atnaujinimai: Su internetine platforma naujos funkcijos ar atnaujinimai gali būti pridėti reguliariai, užtikrinant, kad visada turėtumėte naujausių įrankių ir pataisymų.

Be to, Mokslinis skaičiuotuvas online 991 Plus suteikia intuityvią vartotojo sąsają, padedančią vartotojams lengvai pereiti nuo fizinio skaičiuotuvo prie internetinio varianto neprarandant produktyvumo.

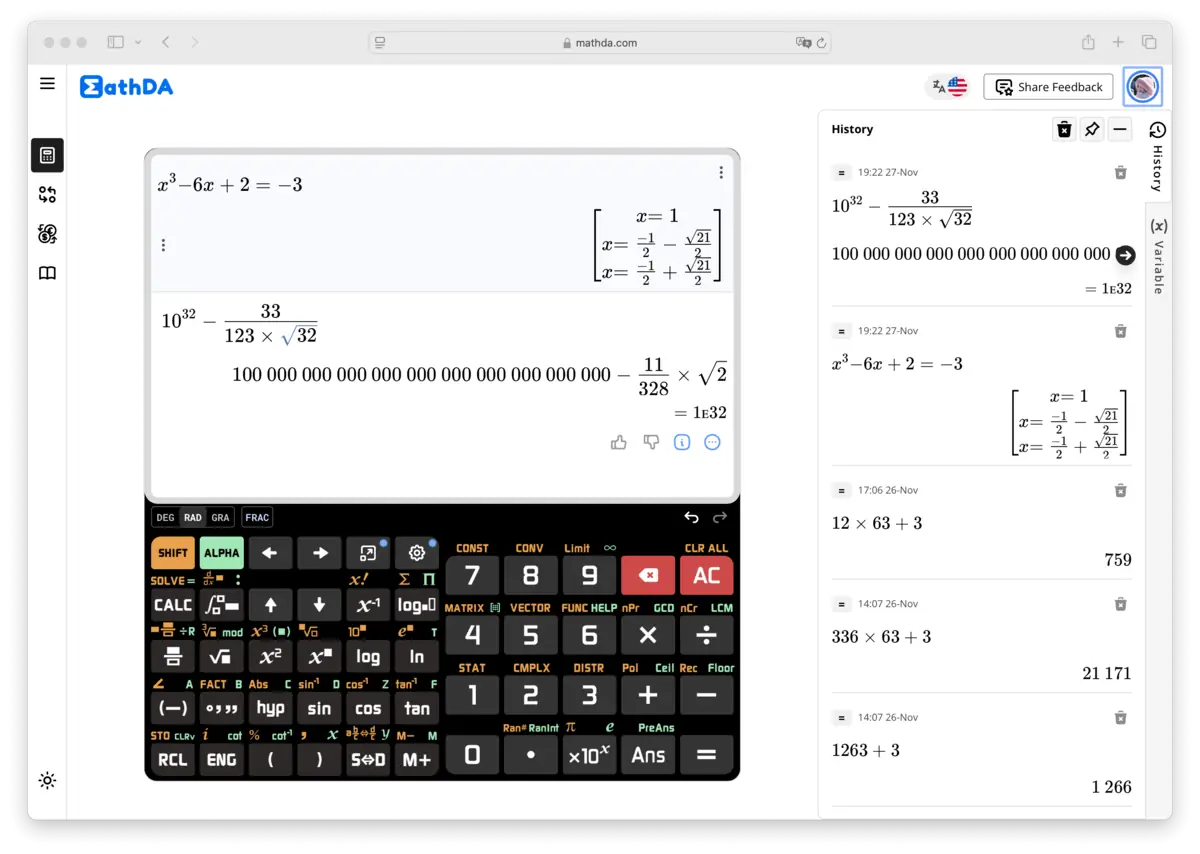
5. Mokslinio Skaičiuotuvo Taikymai

Moksliniai skaičiuotuvai turi daugybę panaudojimo sričių:

• Švietimas: Jie yra nepakeičiami STEM studentams, padedant įvairuose dalykuose nuo algebros iki fizikos. Pažangios Mokslinis skaičiuotuvas online 991 Plus funkcijos ypač naudingos aukštojo mokslo srityje, kur reikalingi sudėtingi problemų sprendimai.
• Profesinis Naudojimas: Inžinerijoje, fizikoje ir statistinėje analizėje moksliniai skaičiuotuvai leidžia beveik nesibaigiantį sudėtingų problemų sprendimų spektrą techninėse srityse. Patobulintos 991 Plus modelio funkcijos dar labiau stiprina šiuos profesionalius poreikius.
• Kasdienis Naudojimas: Moksliniai skaičiuotuvai gali būti naudojami namų ir finansiniams skaičiavimams, tokiems kaip paskolų palūkanų ar valiutų keitimų skaičiavimas, todėl jie naudingi net ir už mokymo bei profesinių kontekstų ribų.

Galimybė šiuos uždavinius atlikti internete užtikrina, kad vartotojai niekada nebūtų be esminių skalicinacinių įrankių, sutaupant laiko ir pastangų.

6. Patarimai kaip maksimaliai išnaudoti Mokslinį skaičiuotuvą online 991 Plus

Kad gautumėte kuo daugiau naudos iš Mokslinis skaičiuotuvas online 991 Plus, apsvarstykite šiuos dalykus:

• Susipažinkite su Sąsaja: Skirkite laiko susipažinimui su visomis galimomis funkcijomis ir spartiesiems klavišams, kad padidintumėte skaičiavimo efektyvumą.
• Reguliarus Praktikavimas: Nuolat naudokite skaičiuotuvą, kad taptumėte įgudus naudotis įvairiems uždaviniams.
• Naudokite Internetinius Šaltinius: Kreipkitės į mokymo medžiagą ir gaires, kurios aiškina, kaip atlikti specifinius skaičiavimus, ypač sudėtingas funkcijas, kaip matricų veiksmus ar integralus.

7. Išvados

Mūsų internetinis mokslinis skaičiuotuvas yra galingas ir universalus įrankis, kuris suteikia fizinio mokslinio skaičiuotuvo galimybes jūsų naršyklėje. Nesvarbu, ar esate studentas, inžinierius, ar tiesiog kas nors, kam reikia tikslių skaičiavimų, mes kviečiame jus išbandyti mūsų įrankį.

Mokslinis skaičiuotuvas online 991 Plus siūlo dar daugiau pažangių funkcijų, atitinkančių akademinių ir profesinių aplinkų reikliausius poreikius. Naudodamiesi mūsų internetinio skaičiuotuvo prieinamumu, prieinamumu ir universalumu, nėra būtinybės investuoti į fizinį įrenginį. Ištirkite šį įrankį kartu su kitais ištekliais, esančiais mūsų svetainėje, ir atraskite, kaip mūsų mokslinis skaičiuotuvas gali palaikyti jūsų mokslinius ir profesinius tikslus.

Dažniausiai Užduodami Klausimai (DUK) apie Mokslinius Skaičiuotuvus Internete

1. Kas yra mokslinis skaičiuotuvas internete?

Mokslinis skaičiuotuvas internete yra internetinė priemonė, leidžianti vartotojams atlikti sudėtingus matematinius skaičiavimus, tokius kaip trigonometrija, logaritmai, eksponentės, statistika ir daugiau. Paprastai jis imituoja fizinių mokslinių skaičiuotuvų funkcionalumą.

2. Kaip galiu pasiekti mokslinį skaičiuotuvą internete?

Jūs galite pasiekti mokslinį skaičiuotuvą internete per įvairias svetaines ar programas. Tiesiog ieškokite "MathDA mokslinis skaičiuotuvas" savo interneto naršyklėje ir pasirinkite tą, kuri atitinka jūsų poreikius.

3. Ar man reikia atsisiųsti ar įdiegti programinę įrangą, kad ją naudoti?

Ne, internetiniai moksliniai skaičiuotuvai veikia tiesiai naršyklėje, nereikia atsisiųsti ar įdiegti.

4. Kokius skaičiavimus galiu atlikti?

Jūs galite atlikti plačiai įvairius skaičiavimus, įskaitant:

• Pagrindinę aritmetiką (sudėtis, atimtis, daugyba, dalyba)
• Trigonometrijos funkcijas (sin, kos, tan ir kt.)
• Logaritminės ir eksponentinės skaičiavimus
• Statistines funkcijas (vidurkis, standartinis nuokrypis, regresija ir kt.)
• Kompleksiniai skaičiai ir matricų operacijos
• Mato vienetų konvertavimai

5. Ar jis nemokamas naudoti?

Mūsų internetinis mokslinis skaičiuotuvas yra nemokamas naudoti.

6. Ar galime grafikuoti funkcijas naudojant mokslinį skaičiuotuvą internete?

Taip, mūsų moksliniai skaičiuotuvai internete turi grafavimosi funkcijas. Jūs galite nubraižyti funkcijas geresniam supratimui.

7. Ar internetinis mokslinis skaičiuotuvas yra tikslus?

Taip, mūsų internetiniai skaičiuotuvai yra labai tikslūs.

8. Ar galiu jį naudoti savo išmaniajame telefone ar planšetėje?

Taip, mūsų mokslinis skaičiuotuvas internete paprastai yra pritaikytas mobiliesiems įrenginiams ir gerai veikia išmaniuosiuose telefonuose ir planšetėse.

9. Ar internetiniai moksliniai skaičiuotuvai saugūs?

Taip, mūsų mokslinis skaičiuotuvas internete yra saugus naudojimui.

10. Ar jis gali spręsti lygtis ar rodyti žingsnis po žingsnio sprendimus?

Taip, mūsų internetinis skaičiuotuvas gali spręsti lygtis.

11. Ar yra kokių nors apribojimų, kai naudojami moksliniai skaičiuotuvai internete?

Mūsų mokslinis skaičiuotuvas internete yra galingas.

12. Ar studentai gali juos naudoti egzaminų metu?

Tai priklauso nuo egzaminų taisyklių. Kai kurie egzaminai leidžia naudoti internetinius įrankius, o kiti riboja jų naudojimą, siekiant išvengti sukčiavimo.

13. Ar mūsų mokslinis skaičiuotuvas internete veikia kaip tikras skaičiuotuvas?

Taip, mūsų mokslinis skaičiuotuvas internete veikia kaip tikri moksliniai skaičiuotuvai, atkartuojant fizinių skaičiuotuvų elgesį.