Istorija
History is currently empty

    Prijavite se da biste koristili sve funkcije

    • Istorija računanja
    • Sačuvaj i sinhronizuj podešavanja
    • Iskoristi napredne funkcije
    Varijabla

    Krajnji Vodič za Naučne Kalkulatore

    1. Uvod

    Naučni kalkulator je moćan alat osmišljen za složene matematičke proračune, koji prevazilaze mogućnosti osnovnog kalkulatora. On ne vrši samo osnovne aritmetičke operacije, već i napredne funkcije potrebne za visoko obrazovanje, inženjerstvo, nauku i matematiku. Naučni kalkulatori su neprocenjivi u obrazovnim i profesionalnim okruženjima, jer studentima i stručnjacima omogućavaju precizne izračune.

    Pravi Naučni Kalkulator

    Pored fizičkih kalkulatora, na našem sajtu postoji praktičan naučni kalkulator na mreži. Ovaj alat odražava funkcije tradicionalnih naučnih kalkulatora i dodaje prednost pristupačnosti sa bilo kog uređaja sa internet vezom, što osigurava da su proračuni uvek na dohvat ruke. Napredna verzija, Naučni Kalkulator Online 991 Plus, nudi mnoštvo funkcija za složene matematičke operacije, zadovoljavajući potrebe studenata, edukatora i profesionalaca.

    Online Naučni Kalkulator

    2. Ključne Karakteristike Naučnog Kalkulatora

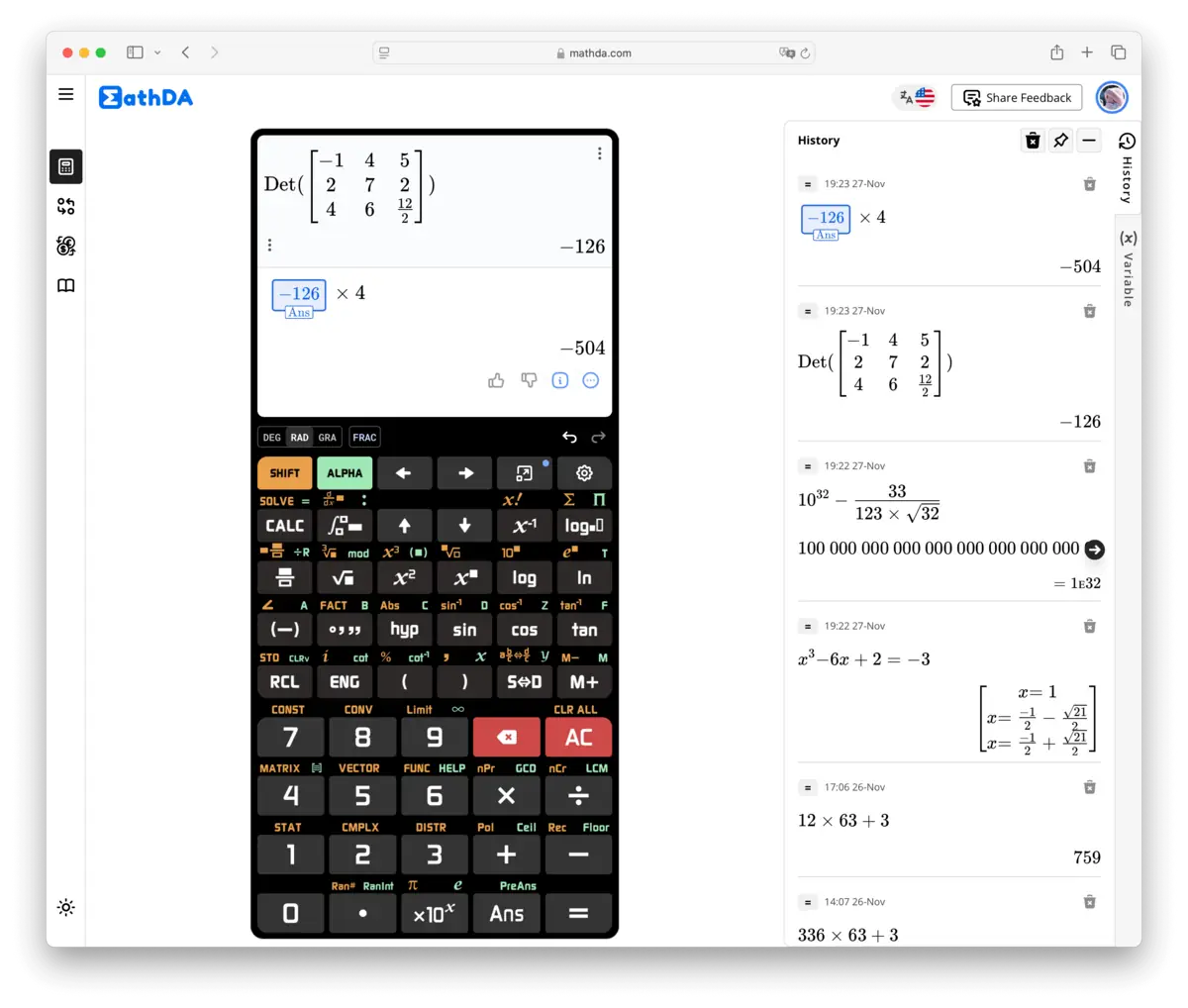
    Naučni kalkulatori su opremljeni različitim funkcijama koje ih čine superiornim u odnosu na osnovne kalkulatore. Evo pregleda tih ključnih karakteristika:

    • Osnovna Aritmetika: Obavlja standardne operacije kao što su sabiranje, oduzimanje, množenje i deljenje, što je ključno za svakodnevne proračune.
    • Eksponencijalne Funkcije: Izračuni koji uključuju eksponente i korene su olakšani. Ovo uključuje kvadrate, kvadratne korene i druge stepene.
    • Trigonometrijske Funkcije: Funkcije kao što su sinus, kosinus i tangens (i njihove inverzne vrednosti) su ključne za rešavanje problema iz geometrije i fizike.
    • Logaritamske i Eksponencijalne Funkcije: Naučni kalkulatori rukovode i prirodnim (ln) i logaritamskim proračunima baze 10, kao i eksponencijalnim operacijama.
    • Proračuni sa Kompleksnim Brojevima: Za naprednije studije, ovi kalkulatori mogu obavljati proračune sa kompleksnim brojevima, što je ključno u inženjerstvu i fizici.
    • Statističke Funkcije: Funkcije za izračunavanje proseka, standardne devijacije i drugih statističkih vrednosti su uključene, što olakšava rad studentima i profesionalcima.
    • Memorijske Funkcije: Vrednosti se mogu skladištiti i ponovo koristiti, što pojednostavljuje rad sa višestepenim problemima.

    Naučni Kalkulator Online 991 Plus poboljšava ove sposobnosti nudeći dodatne funkcije kao što su matrični proračuni, integracija, diferencijacija i rešavanje jednačina, čineći ga sveobuhvatnim alatom za složene matematičke zadatke.

    Pravi Naučni Kalkulator

    3. Razumevanje Naučnog Kalkulatora 991 Plus

    Naučni Kalkulator 991 Plus je napredni alat koji koriste studenti i stručnjaci širom sveta. Ključne komponente i karakteristike uključuju:

    • Korisnički Interfejs: Dizajniran da bude intuitivan, omogućava korisnicima jednostavno snalaženje kroz složene operacije.
    • Napredne Matematičke Funkcije: Podržava dodatne funkcije poput hiperbolične trigonometrije, vektorskih proračuna i statističke regresije, idealne za napredne studije i profesionalne zadatke.

    Njegova svestranost i sposobnost rukovanja složenim operacijama čine ga vrhunskim izborom za sve koji rade s intenzivnim proračunima.

    4. Prednosti Korišćenja Naučnog Kalkulatora na Mreži

    Naš online naučni kalkulator nudi nekoliko prednosti u odnosu na tradicionalne kalkulatore:

    • Pristupačnost: Dostupan je bilo kada i bilo gde putem našeg sajta, osiguravajući korisnicima pristup osnovnim matematičkim alatima gde god da se nalaze.
    • Troškovna Efikasnost: Za razliku od fizičkog kalkulatora, naša online verzija je besplatna za korišćenje, štedeći vas od kupovine zasebnog uređaja.
    • Kompatibilnost sa Uređajima: Bilo da ste na desktopu, mobilnom ili tabletu, naš online kalkulator je dizajniran da besprekorno radi na svim platformama.
    • Redovna Ažuriranja: Sa online platformom, nove funkcije ili ažuriranja se mogu redovno dodavati, osiguravajući da uvek imate pristup najnovijim alatima i popravkama bugova.

    Uz to, Naučni Kalkulator Online 991 Plus pruža intuitivan korisnički interfejs, što olakšava korisnicima prelazak sa fizičkog kalkulatora na online verziju bez gubitka produktivnosti.

    Online Naučni Kalkulator

    5. Primene Naučnog Kalkulatora

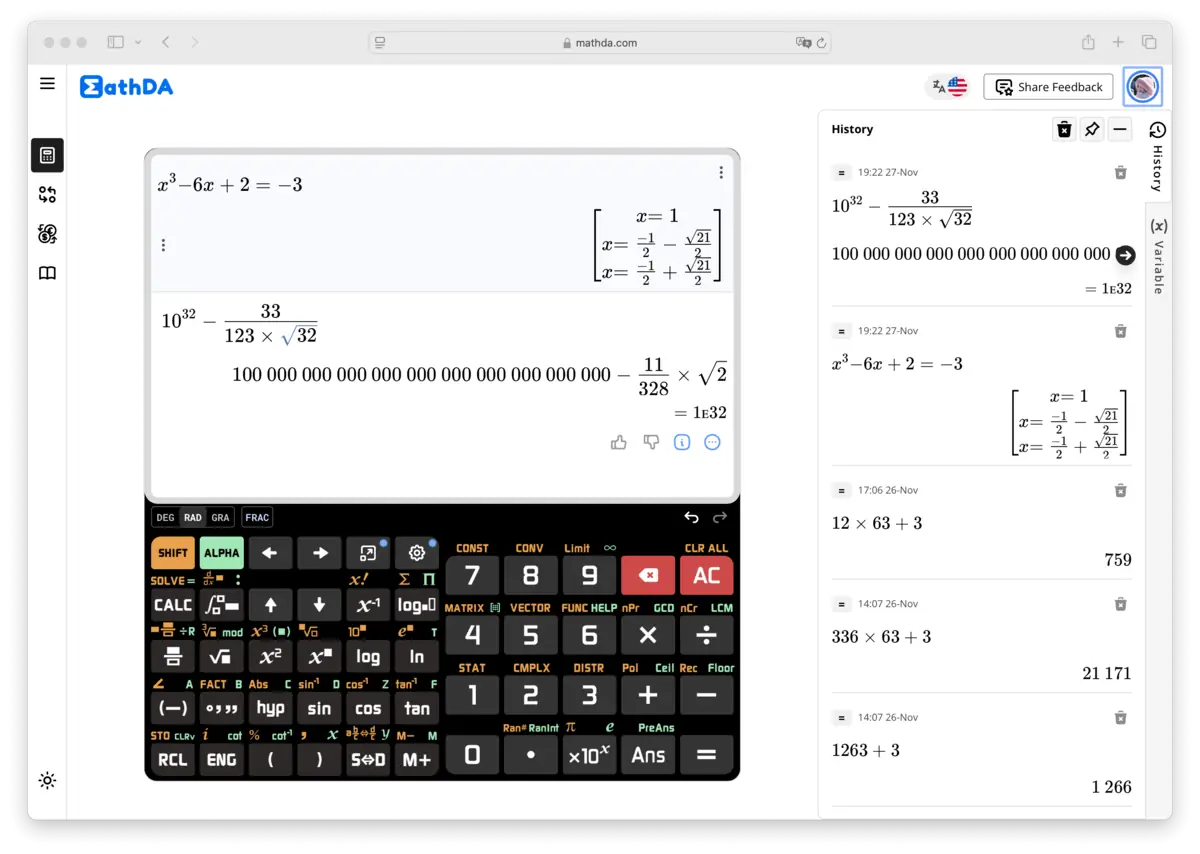
    Naučni kalkulatori služe širokom spektru primena:

    • Obrazovanje: Neizbežni su za STEM studente, pomažući u predmetima od algebre do fizike. Napredne funkcije Naučnog Kalkulatora Online 991 Plus posebno su korisne za visoko obrazovanje, gde je potrebno složeno rešavanje problema.
    • Profesionalna Upotreba: U inženjerstvu, fizici i statističkoj analizi, naučni kalkulatori omogućavaju kompleksno rešavanje problema koji su potrebni u mnogim tehničkim oblastima. Poboljšane funkcije modela 991 Plus dodatno podržavaju ove profesionalne zahteve.
    • Svakodnevna Upotreba: Naučni kalkulatori se mogu koristiti za kućne i finansijske proračune, kao što su izračunavanje kamate na zajam ili konverzije valuta, što ih čini korisnim čak i izvan akademskog i profesionalnog okruženja.

    Fleksibilnost za obavljanje ovih zadataka online osigurava da korisnici nikada nisu bez svojih esencijalnih alata za proračunavanje, štedeći vreme i trud.

    6. Saveti za Maksimalno Korišćenje Naučnog Kalkulatora Online 991 Plus

    Da biste izvukli maksimum iz Naučnog Kalkulatora Online 991 Plus, razmotrite sledeće:

    • Upoznajte se s Interfejsom: Provedite vreme upoznajući sve dostupne funkcije i prečice kako biste poboljšali efikasnost proračuna.
    • Redovno Vežbajte: Koristite kalkulator redovno kako biste postali vešti u korišćenju za različite zadatke.
    • Iskoristite Online Resurse: Pristupite tutorijalima i vodičima koji objašnjavaju kako se obavljaju specifični proračuni, posebno složene funkcije kao što su matrične operacije ili integracija.

    7. Zaključak

    Naš online naučni kalkulator je moćan i svestran alat koji donosi mogućnosti fizičkog naučnog kalkulatora uz pogodnost vašeg pretraživača. Bilo da ste student, inženjer, ili jednostavno neko kome su potrebni precizni proračuni, ohrabrujemo vas da ga isprobate.

    Naučni Kalkulator Online 991 Plus nudi još naprednije funkcije koje zadovoljavaju rigorozne zahteve akademskog i profesionalnog okruženja. Uz pristupačnost, povoljnost i svestranost našeg online kalkulatora, nema potrebe da investirate u fizički uređaj. Istražite ovaj alat uz druge resurse dostupne na našem sajtu i otkrijte kako naš naučni kalkulator može podržati vaše obrazovne i profesionalne ciljeve.

    Često Postavljana Pitanja (FAQ) o Online Naučnim Kalkulatorima

    1. Šta je online naučni kalkulator?

    Online naučni kalkulator je alat zasnovan na vebu koji korisnicima omogućava obavljanje složenih matematičkih proračuna kao što su trigonometrija, logaritmi, eksponenti, statistika i drugo. Obično oponaša funkcionalnost fizičkih naučnih kalkulatora.

    2. Kako mogu pristupiti online naučnom kalkulatoru?

    Možete pristupiti online naučnom kalkulatoru putem raznih veb-sajtova ili aplikacija. Jednostavno potražite "MathDA naučni kalkulator" u vašem veb pregledaču i izaberite onaj koji odgovara vašim potrebama.

    3. Da li moram preuzeti ili instalirati softver da bih ga koristio?

    Ne, online naučni kalkulatori rade direktno u vašem pretraživaču bez potrebe za preuzimanjem ili instalacijom.

    4. Kakve proračune mogu izvršavati?

    Možete izvršavati široku paletu proračuna, uključujući:

    • Osnovnu aritmetiku (sabiranje, oduzimanje, množenje, deljenje)
    • Trigonometrijske funkcije (sin, cos, tan, itd.)
    • Logaritamske i eksponencijalne proračune
    • Statističke funkcije (prosek, standardna devijacija, regresija, itd.)
    • Kompleksne brojeve i matrične operacije
    • Jedinice konverzije

    5. Da li je besplatan za korišćenje?

    Naš online naučni kalkulator je besplatan za korišćenje.

    6. Mogu li crtati grafike koristeći online naučni kalkulator?

    Da, naši online naučni kalkulatori uključuju funkcije za crtanje grafikona. Možete crtati funkcije za bolje razumevanje.

    7. Da li je online naučni kalkulator precizan?

    Da, naši online kalkulatori su veoma precizni.

    8. Mogu li ga koristiti na svom pametnom telefonu ili tabletu?

    Da, naš online naučni kalkulator obično je prilagođen mobilnim uređajima i dobro radi na pametnim telefonima i tabletima.

    9. Da li su online naučni kalkulatori bezbedni za korišćenje?

    Da, naš online naučni kalkulator je bezbedan za korišćenje.

    10. Može li rešavati jednačine ili prikazivati rešenja korak po korak?

    Da, naš online kalkulator može rešavati jednačina.

    11. Postoje li neka ograničenja u korišćenju online naučnih kalkulatora?

    Naš online naučni kalkulator je moćan.

    12. Mogu li ga studenti koristiti tokom ispita?

    To zavisi od pravila ispita. Neki ispiti dozvoljavaju korišćenje online alata, dok drugi ograničavaju njihovu upotrebu kako bi se sprečilo varanje.

    13. Da li naš online naučni kalkulator radi kao pravi kalkulator?

    Da, naš online naučni kalkulator funkcioniše kao pravi naučni kalkulatori, replicirajući ponašanje fizičkih kalkulatora.

    Format rezultata
      • Naučna konstanta
      • 1
        Proton mass
        1.67262189821e-27
        kg
        mp
      • 2
        Neutron mass
        1.67492747121e-27
        kg
        mn
      • 3
        Electron mass
        9.1093835611e-31
        kg
        me
      • 4
        Muon mass
        1.88353159448e-28
        kg
        mµ
      • 5
        Bohr radius
        5.291772106712e-11
        m
        a₀
      • 6
        Planck constant
        6.62607004081e-34
        Js
        h
      • 7
        Nuclear magneton
        5.05078369931e-27
        JT-1
        µN
      • 8
        Bohr magneton
        9.27400999457e-24
        JT-1
        µB
      • 9
        Planck constant,rationalized
        1.05457180013e-34
        Js
        ℏ
      • 10
        Fine-structure constant
        0.007297352566417
        α
      • 11
        Classical electron radius
        2.817940322719e-15
        m
        re
      • 12
        Compton wavelength
        2.426310236711e-12
        m
        λc
      • 13
        Proton gyromagnetic ratio
        267522190.018
        s-1T-1
        γp
      • 14
        Proton Compton wavelength
        1.3214098539661e-15
        m
        λcp
      • 15
        Neutron Compton wavelength
        1.3195909048188e-15
        m
        λcn
      • 16
        Rydberg constant
        10973731.56850865
        m-1
        R∞
      • 17
        Atomic mass constant
        1.6605390402e-27
        kg
        u
      • 18
        Proton magnetic moment
        1.410606787397e-26
        JT-1
        µp
      • 19
        Electron magnetic moment
        -9.28476462057e-24
        JT-1
        µe
      • 20
        Neutron magnetic moment
        -9.662365023e-27
        JT-1
        µn
      • 21
        Muon magnetic moment
        -4.490448261e-26
        JT-1
        µµ
      • 22
        Faraday constant
        96485.332895
        Cmol-1
        F
      • 23
        Elementary charge
        1.602176620898e-19
        C
        e
      • 24
        Avogadro constant
        6.02214085774e+23
        mol-1
        NA
      • 25
        Boltzmann constant
        1.3806485279e-23
        JK-1
        k
      • 26
        Molar volume of ideal
        0.02271094713
        m3mol-1
        Vm
      • 27
        Molar gas constant
        8.3144598484848
        Jmol-1K-1
        R
      • 28
        Speed of light in vacuum
        299792458
        ms-1
        C₀
      • 29
        First radiation constant
        3.74177179046e-16
        Wm2
        C₁
      • 30
        Second radiation constant
        0.014387773683
        mK
        C₂
      • 31
        Stefan-Boltzmann constant
        5.67036713e-8
        Wm-2K-4
        σ
      • 32
        Electric constant
        8.854187817e-12
        Fm-1
        ε₀
      • 33
        Magnetic constant
        0.00000125663706
        NA-2
        µ₀
      • 34
        Magnetic flux quantum
        2.06783383113e-15
        Wb
        φ₀
      • 35
        Standard acceleration of gravity
        9.80665
        ms-2
        g
      • 36
        Conductance quantum
        0.00007748091731018
        S
        G₀
      • 37
        Characteristic impedance of vacuum
        376.730313461
        Ω
        Z₀
      • 38
        Celsius temperature
        273.15
        K
        t
      • 39
        Newtonian constant of gravitation
        6.6740831e-11
        m3kg-1s-2
        G
      • 40
        Standard atmosphere
        101325
        Pa
        atm
      Metričke konverzije
      • 1
        in→cm
        inch (in) ► centimeter (cm)
      • 2
        cm→in
        centimeters to inches
      • 3
        ft→m
        foot (ft) ► meter (m)
      • 4
        m→ft
        meters to feet
      • 5
        yd→m
        yard (yd) ► meter (m)
      • 6
        m→yd
        meters to yards
      • 7
        mile→km
        mile (mi) ► kilometer (km)
      • 8
        km→mile
        kilometers to miles
      • 9
        n mile→m
      • 10
        m→n mile
      • 11
        acre→m²
        acre (based on U.S. survey foot)► square meter (m²)
      • 12
        m²→acre
        square meters to acres
      • 13
        gal(US)→L
        gallon (U.S.) (gal) ► liter (L)
      • 14
        L→gal(US)
        liters to US gallons
      • 15
        gal(UK)→L
        gallon [Canadian and U.K. (Imperial)] (gal) ► liter (L)
      • 16
        L→gal(UK)
        Liters to UK gallons
      • 17
        pc→km
        parsec (pc) ► meter (m)
      • 18
        km→pc
      • 19
        km/h→m/s
        kilometer per hour (km / h) ► meter per second (m / s)
      • 20
        m/s→km/h
        meters/second to kilometers/hour
      • 21
        oz→g
        ounce (avoirdupois) (oz) ► gram (g)
      • 22
        g→oz
        grams to ounces
      • 23
        lb→kg
        pound (troy or apothecary) (lb) ► kilogram (kg)
      • 24
        kg→lb
        kilograms to pounds
      • 25
        atm→Pa
        atmosphere, standard (atm) ► pascal (Pa)
      • 26
        Pa→atm
        Pascals to atmospheres
      • 27
        mmHg→Pa
        millimeter of mercury, conventional (mmHg) ► pascal (Pa)
      • 28
        Pa→mmHg
        Pascals to millimeters of mercury
      • 29
        hp→kW
        horsepower (550 ft · lbf / s) (hp) ► kilowatt (kW)
      • 30
        kW→hp
        kilowatt (kW) ► horsepower (550 ft · lbf / s) (hp)
      • 31
        kgf/cm²→Pa
        kilogram-force per square centimeter(kgf/cm2)) ► pascal (Pa)
      • 32
        Pa→kgf/cm²
      • 33
        kgf•m→J
      • 34
        J→kgf•m
      • 35
        lbf/in²→kPa
        pound-force per square inch (psi) (lbf/in2) ► pascal (Pa)
      • 36
        kPa→lbf/in²
      • 37
        °F→°C
        degree Fahrenheit (temperature) (ºF) ................... degree Celsius (ºC)
      • 38
        °C→°F
        Celsius to Farenheit
      • 39
        J→cal
        joule (J) ► calorieIT (calIT)
      • 40
        cal→J
        calorieIT (calIT) ► joule (J)
      Hyperbolic
      • 1
        Sinh(value)
        Hyperbolic sine
      • 2
        Cosh(value)
        Hyperbolic cosine
      • 3
        Tanh(value)
        Hyperbolic tangent
      • 4
        Coth(value)
        Hyperbolic cotangent
      • 5
        Sech(value)
        Hyperbolic secant
      • 6
        Csch(value)
        Hyperbolic cosecant
      • 7
        ArcSinh(value)
        Hyperbolic arcsine
      • 8
        ArcCosh(value)
        Hyperbolic arccosine
      • 9
        ArcTanh(value)
        Hyperbolic arctangent
      • 10
        ArcCoth(value)
        Inverse hyperbolic cotangent
      • 11
        ArcSech(value)
        Inverse hyperbolic secant
      • 12
        ArcCsch(value)
        Inverse hyperbolic cosecant
        • Additional trigonometric functions
      • 13
        Cot(expr)
        the cotangent function
      • 14
        ArcCot(z)
        returns the inverse cotangent of z
      • 15
        Sec(z)
        returns the secant of z
      • 16
        ArcSec(z)
        returns the inverse secant of z
      • 17
        Csc(z)
        returns the cosecant of z
      • 18
        ArcCsc(z)
        returns the inverse cosecant of z
      COMPLEX
      • 1
        Arg
        Argument of the complex number
      • 2
        Conjugate
        Conjugate of the complex number
      • 3
        Re
        Real component
      • 4
        Im
        Imaginary component
      • 5
        ▸r∠φ
        Displays the result in polar form
      • 6
        ▸a+bi
        Displays the result in rectangular form
      • 7
        Abs
        Returns the magnitude (modulus)
      Podešavanja
      Potvrda resetovanja podešavanja
      Ova akcija će trajno izbrisati vaša podešavanja i resetovati ih na podrazumevano
      Format decimalnog broja
      Matrica
      • 1
        Umetni matricu
      • 2
        Det(matrix)
        Calculates the determinant
      • 3
        Inverse(matrix)
        Compute the inverse of the matrix
      • 4
        MatrixRank(matrix)
        returns the rank of matrix
      • 5
        Transpose(matrix)
        Transposes the matrix
      • 6
        IdentityMatrix(dimension)
        Returns the identity matrix
      • 7
        RowReduce(matrix)
        Return the reduced row-echelon form
      • 8
        CharacteristicPolynomial(matrix, var)
        Computes the characteristic polynomial of a matrix for the variable var
      • 9
        Diagonal(list)
        Computes the diagonal vector of the matrix
      • 10
        DiagonalMatrix(list)
        Gives a matrix with the values in list on its diagonal and zeroes elsewhere
      • 11
        Eigenvalues(matrix)
        Get the numerical eigenvalues of the matrix
      • 12
        Eigenvectors(matrix)
        Get the numerical eigenvectors of the matrix
      • 13
        LeastSquares(matrix, right)
        Solves the linear least-squares problem 'matrix.x = right'
      • 14
        LinearSolve(matrix, right)
        Solves the linear equation system 'matrix.x = right' and returns one corresponding solution x
      • 15
        LUDecomposition(matrix)
        Calculate the LUP-decomposition of a square matrix
      • 16
        NullSpace(matrix)
        Returns a list of vectors that span the nullspace of the matrix
      • 17
        PseudoInverse(matrix)
        Computes the Moore-Penrose pseudoinverse of the matrix. If matrix is invertible, the pseudoinverse equals the inverse
      • 18
        SingularValueDecomposition(matrix)
        Calculates the singular value decomposition for the matrix
      Umetni matricu
      Dimenzije matrice
      ✖
      1
      2
      3
      4
      5
      6
      7
      1
      2
      3
      4
      5
      6
      7
      Promeni izgled kalkulatora
      Koji simbol bi taster , trebalo da predstavlja?
      * Možete kasnije promeniti konfiguraciju u podešavanjima
      Prijavite se da biste koristili sve funkcije
      • Istorija računanja
      • Sačuvaj i sinhronizuj podešavanja
      • Iskoristi napredne funkcije
      Povratne informacije o izračunavanju
      Navođenje vašeg emaila pomaže nam da vas kontaktiramo kako bismo efikasnije rešili vaš problem (opciono)