Den Ultimata Guiden till Vetenskapliga Kalkylatorer

1. Introduktion

En vetenskaplig kalkylator är ett kraftfullt verktyg utformat för komplexa matematiska beräkningar som går långt utöver kapaciteterna hos en vanlig kalkylator. Den utför inte bara grundläggande aritmetik utan också avancerade funktioner som är viktiga för högre utbildning, teknik, vetenskap och matematik. Vetenskapliga kalkylatorer är ovärderliga i utbildnings- och professionella miljöer, och hjälper studenter och yrkesverksamma med exakta beräkningar.

Förutom fysiska kalkylatorer finns det en praktisk vetenskaplig kalkylator online på vår webbplats. Detta verktyg speglar funktionerna hos traditionella vetenskapliga kalkylatorer och har fördelen av att vara tillgängligt från vilken internetansluten enhet som helst, och säkerställer att beräkningar alltid finns tillgängliga. Vetenskaplig Kalkylator Online 991 Plus är en avancerad version som erbjuder en uppsjö av funktioner anpassade för komplexa matematiska operationer, och tillgodoser behoven hos studenter, lärare och yrkesverksamma.

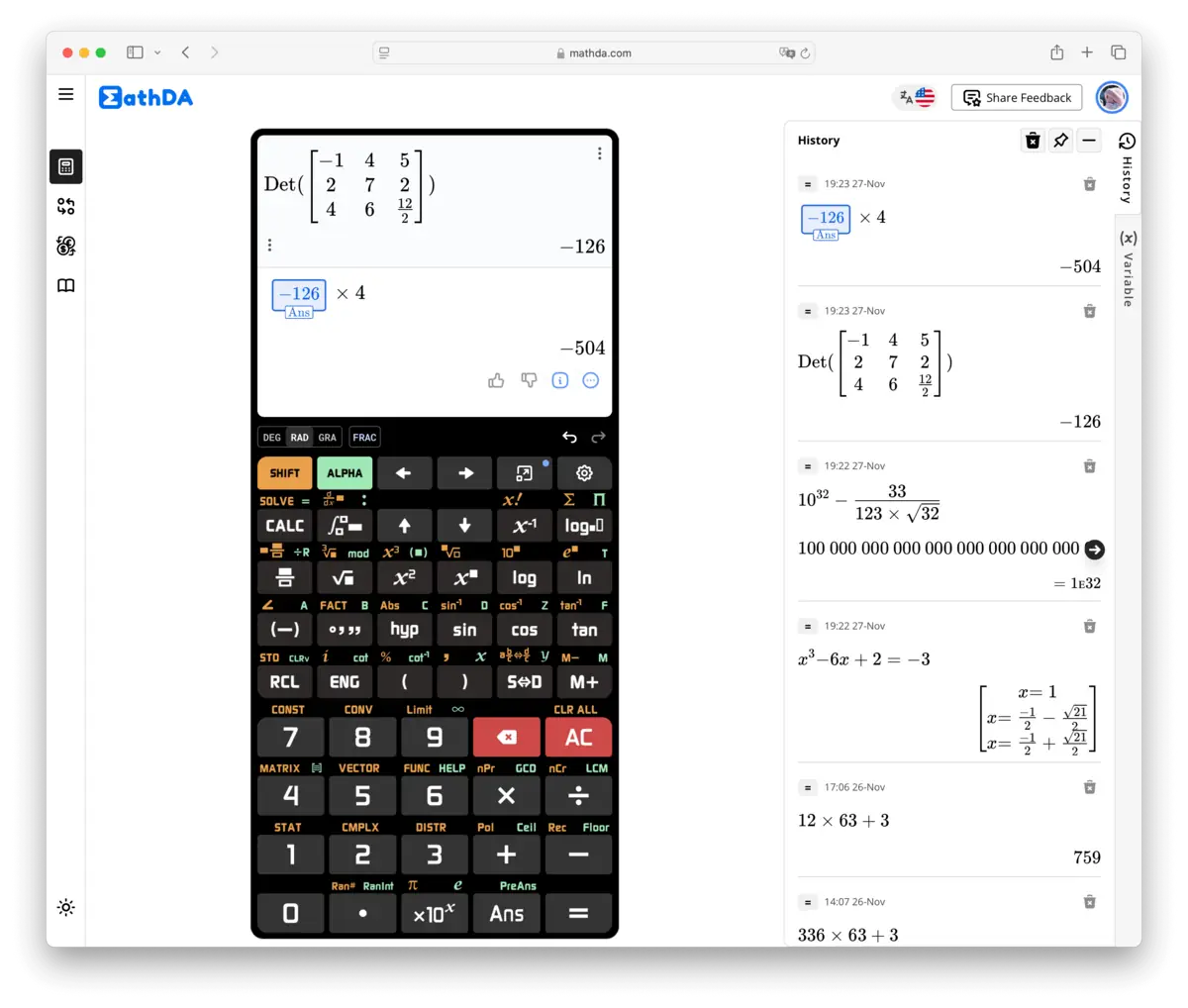
2. Nyckelfunktioner hos en Vetenskaplig Kalkylator

Vetenskapliga kalkylatorer är fullpackade med en mängd funktioner som gör dem överlägsna enkla kalkylatorer. Här är en översikt över dessa nyckelfunktioner:

• Grundläggande Aritmetik: Utför standardoperationer som addition, subtraktion, multiplikation och division, vilka är nödvändiga för vardagliga beräkningar.
• Exponentiella Funktioner: Beräkningar med exponenter och rötter är enkla. Detta inkluderar kvadrater, kvadratrötter och andra potenser.
• Trigonometriska Funktioner: Funktioner som sinus, cosinus och tangens (och deras inverser) är viktiga för att lösa problem i geometri och fysik.
• Logaritmiska och Exponentiella Funktioner: Vetenskapliga kalkylatorer hanterar både naturliga (ln) och bas-10 logaritmiska beräkningar, liksom exponentiella operationer.
• Beräkningar med Komplexa Tal: För mer avancerade studier kan dessa kalkylatorer utföra beräkningar med komplexa tal, vilket är viktigt inom teknik och fysik.
• Statistiska Funktioner: Funktioner för att beräkna medelvärde, standardavvikelse och andra statistiska värden ingår, vilket gör det enklare för både studenter och yrkesverksamma.
• Minnesfunktioner: Värden kan sparas och återkallas, vilket effektiviserar arbete med problem som involverar flera steg.

Vetenskaplig Kalkylator Online 991 Plus förbättrar dessa kapaciteter genom att erbjuda ytterligare funktioner som matrisberäkningar, integration, differentiering och ekvationslösning, vilket gör den till ett omfattande verktyg för komplexa matematiska uppgifter.

3. Förstå Vetenskaplig Kalkylator 991 Plus

Vetenskaplig Kalkylator 991 Plus är ett avancerat verktyg som används av studenter och yrkesverksamma världen över. Viktiga komponenter och funktioner inkluderar:

• Användargränssnitt: Utformat för att vara intuitivt, vilket tillåter användare att enkelt navigera komplexa operationer.
• Avancerade Matematiska Funktioner: Stödjer ytterligare funktioner som hyperbolisk trigonometri, vektorberäkningar och statistisk regression, idealiskt för avancerade studier och professionella uppgifter.

Dess mångsidighet och förmåga att hantera komplexa operationer gör den till ett förstahandsval för alla som arbetar med omfattande beräkningar.

4. Fördelar med att Använda en Vetenskaplig Kalkylator Online

Vår vetenskapliga kalkylator online erbjuder flera fördelar jämfört med traditionella kalkylatorer:

• Tillgänglighet: Tillgänglig när som helst och var som helst via vår webbplats, vilket säkerställer att användare alltid har tillgång till viktiga matematiska verktyg.
• Kostnadseffektivt: Till skillnad från en fysisk kalkylator är vår onlineversion gratis att använda, vilket sparar kostnaden för att köpa en separat enhet.
• Enhetskompatibilitet: Oavsett om du använder en dator, mobil eller surfplatta är vår onlinekalkylator utformad för att fungera sömlöst på alla plattformar.
• Regelbundna Uppdateringar: Med en onlineplattform kan nya funktioner eller uppdateringar läggas till regelbundet, vilket säkerställer att du alltid har tillgång till de senaste verktygen och buggfixarna.

Dessutom erbjuder Vetenskaplig Kalkylator Online 991 Plus ett intuitivt användargränssnitt, vilket gör det enkelt för användare att övergå från en fysisk kalkylator till en onlineversion utan att förlora produktivitet.

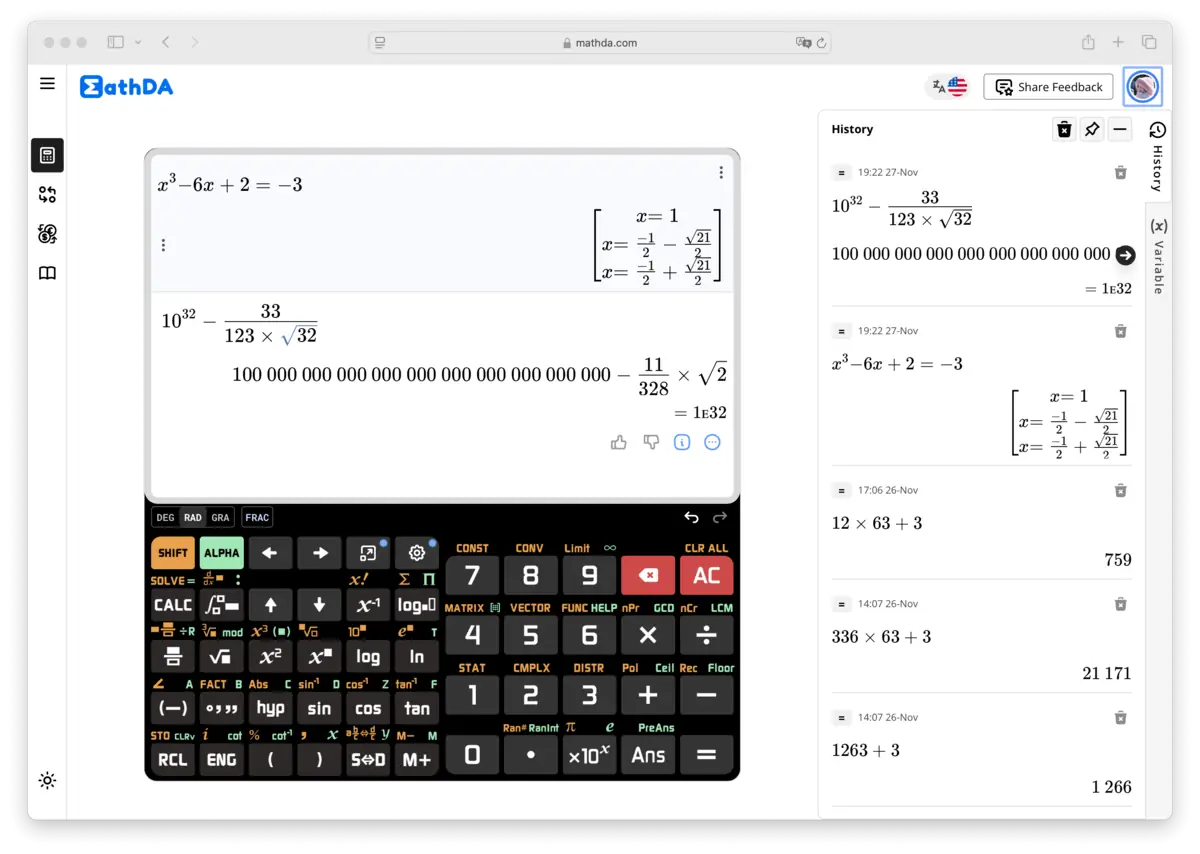
5. Användningsområden för en Vetenskaplig Kalkylator

Vetenskapliga kalkylatorer används inom en rad olika områden:

• Utbildning: De är oumbärliga för STEM-studenter och hjälper inom ämnen från algebra till fysik. De avancerade funktionerna hos Vetenskaplig Kalkylator Online 991 Plus är särskilt fördelaktiga för högre utbildning där komplex problemlösning krävs.
• Professionell Användning: Inom ingenjörsvetenskap, fysik och statistisk analys möjliggör vetenskapliga kalkylatorer komplex problemlösning som behövs inom många tekniska områden. De utökade funktionerna hos 991 Plus-modellen stödjer dessa professionella behov ytterligare.
• Vardaglig Användning: Vetenskapliga kalkylatorer kan användas för hushålls- och finansiella beräkningar, såsom att beräkna låneräntor eller valutakonverteringar, vilket gör dem användbara även utanför akademiska och professionella sammanhang.

Möjligheten att utföra dessa uppgifter online garanterar att användare aldrig är utan sina viktiga beräkningsverktyg, och sparar både tid och ansträngning.

6. Tips för att Maximera Användningen av Vetenskaplig Kalkylator Online 991 Plus

För att få ut det mesta av Vetenskaplig Kalkylator Online 991 Plus, överväg följande:

• Bekanta dig med Gränssnittet: Lägg tid på att lära känna alla tillgängliga funktioner och genvägar för att förbättra beräkningseffektiviteten.
• Regelbunden Träning: Använd kalkylatorn regelbundet för att bli skicklig i att använda den för en mängd olika uppgifter.
• Använd Onlineresurser: Få tillgång till handledningar och guider som förklarar hur man utför specifika beräkningar, särskilt komplexa funktioner som matrisoperationer eller integration.

7. Slutsats

Vår vetenskapliga kalkylator online är ett kraftfullt och mångsidigt verktyg som för med sig kapaciteterna hos en fysisk vetenskaplig kalkylator till din webbläsares bekvämlighet. Oavsett om du är student, ingenjör, eller bara behöver exakta beräkningar, uppmuntrar vi dig att prova den.

Vetenskaplig Kalkylator Online 991 Plus erbjuder ännu mer avancerade funktioner som möter de stränga kraven från akademiska och professionella miljöer. Med tillgängligheten, prisvärdheten och mångsidigheten hos vår onlinekalkylator, finns det inget behov av att investera i en fysisk enhet. Utforska detta verktyg tillsammans med de andra resurserna som finns tillgängliga på vår webbplats och upptäck hur vår vetenskapliga kalkylator kan stödja dina utbildnings- och professionella mål.

Vanliga Frågor (FAQ) om Vetenskapliga Kalkylatorer Online

1. Vad är en vetenskaplig kalkylator online?

En vetenskaplig kalkylator online är ett webbaserat verktyg som tillåter användare att utföra komplexa matematiska beräkningar såsom trigonometri, logaritmer, exponenter, statistik och mer. Den efterliknar vanligtvis funktionaliteten hos fysiska vetenskapliga kalkylatorer.

2. Hur får jag åtkomst till en vetenskaplig kalkylator online?

Du kan få åtkomst till en vetenskaplig kalkylator online via olika webbplatser eller appar. Sök helt enkelt efter "MathDA vetenskaplig kalkylator" i din webbläsare, och välj en som passar dina behov.

3. Behöver jag ladda ner eller installera programvara för att använda den?

Nej, vetenskapliga kalkylatorer online fungerar direkt i din webbläsare utan att kräva nedladdningar eller installationer.

4. Vilken typ av beräkningar kan jag utföra?

Du kan utföra en mängd olika beräkningar, inklusive:

• Grundläggande aritmetik (addition, subtraktion, multiplikation, division)
• Trigonometriska funktioner (sin, cos, tan, etc.)
• Logaritmiska och exponentiella beräkningar
• Statistiska funktioner (medelvärde, standardavvikelse, regression, etc.)
• Komplexa tal och matrisoperationer
• Enhetsomvandlingar

5. Är det gratis att använda?

Vår vetenskapliga kalkylator online är gratis att använda.

6. Kan jag rita grafer med en vetenskaplig kalkylator online?

Ja, våra vetenskapliga kalkylatorer online inkluderar graffunktioner. Du kan plotta funktioner för bättre förståelse.

7. Är en vetenskaplig kalkylator online exakt?

Ja, våra onlinekalkylatorer är mycket exakta.

8. Kan jag använda den på min smartphone eller surfplatta?

Ja, vår vetenskapliga kalkylator online är vanligtvis mobilvänlig och fungerar bra på smartphones och surfplattor.

9. Är vetenskapliga kalkylatorer online säkra?

Ja, vår vetenskapliga kalkylator online är säker att använda.

10. Kan den lösa ekvationer eller visa steg-för-steg-lösningar?

Ja, vår onlinekalkylator kan lösa ekvationer.

11. Finns det några begränsningar med att använda vetenskapliga kalkylatorer online?

Vår vetenskapliga kalkylator online är kraftfull.

12. Kan studenter använda dem under prov?

Det beror på reglerna för provet. Vissa prov tillåter användning av onlinverktyg, medan andra begränsar dem för att förhindra fusk.

13. Fungerar vår vetenskapliga kalkylator online som en riktig kalkylator?

Ja, vår vetenskapliga kalkylator online fungerar som riktiga vetenskapliga kalkylatorer, och replikerar beteendet hos fysiska kalkylatorer.