Mwongozo wa Mwisho wa Kalkuleta za Kisayansi

1. Utangulizi

Kalkuleta ya kisayansi ni kifaa chenye nguvu kilichoundwa kwa ajili ya mahesabu magumu ya hisabati yanayozidi uwezo wa kalkuleta ya kawaida. Inaendesha sio tu hesabu za msingi bali pia kazi za juu zinazohitajika kwa elimu ya juu, uhandisi, sayansi, na hisabati. Kalkuleta za kisayansi ni muhimu katika mazingira ya kielimu na kitaaluma, zikisaidia wanafunzi na wataalamu kwa mahesabu sahihi.

Pamoja na kalkuleta za kawaida, kuna kalkuleta ya kisayansi mtandaoni inayopatikana kwenye tovuti yetu. Chombo hiki kinaiga kazi za kalkuleta za kisayansi za asili na kiongeza faida ya kupatikana kutoka kwenye kifaa chochote chenye mtandao, kuhakikisha mahesabu yako yanapopatika kila wakati. Kalkuleta ya Kisayansi Mtandaoni 991 Plus ni toleo la kisasa linalotoa anuwai ya vipengele vinavyofaa kwa operesheni za hesabu ngumu, ikikidhi mahitaji ya wanafunzi, waelimishaji, na wataalamu.

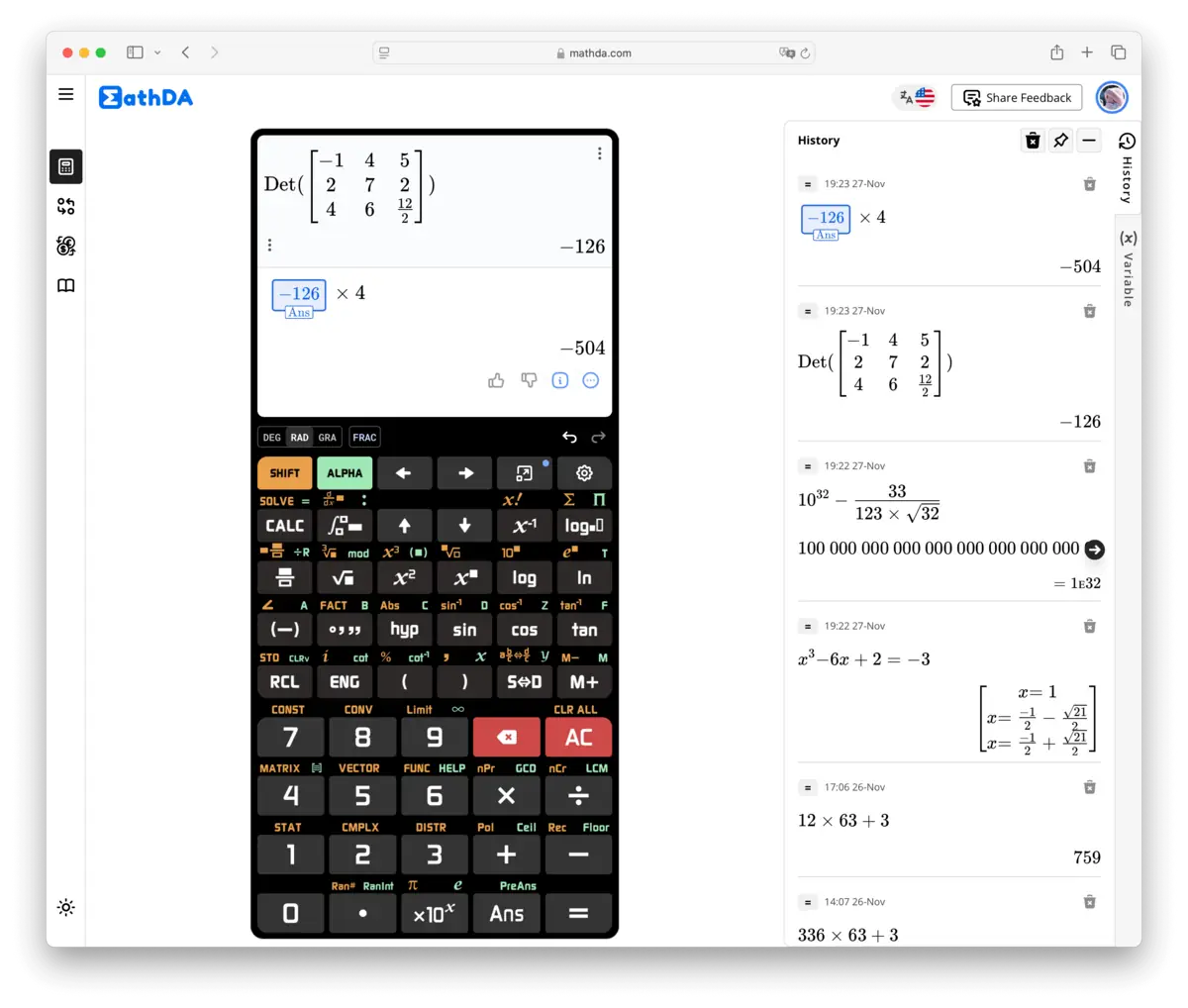
2. Vipengele Muhimu vya Kalkuleta ya Kisayansi

Kalkuleta za kisayansi zinakuja na anuwai ya kazi zinazowafanya kuwa bora zaidi kuliko kalkuleta za kawaida. Hapa kuna muhtasari wa vipengele hivi muhimu:

• Hesabu za Msingi: Inafanya operesheni za kawaida kama kujumlisha, kutoa, kuzidisha, na kugawa, ambazo ni muhimu kwa mahesabu ya kila siku.
• Kazi za Exponential: Mahesabu yanayohusisha viunzi na mizizi hufanywa kuwa rahisi. Hii ni pamoja na kiunzi, mizizi ya mraba, na nguvu nyingine.
• Kazi za Trigonometri: Kazi kama sine, cosine, na tangent (na kinyume chake) ni muhimu kwa kutatua matatizo ya jiometri na fizikia.
• Kazi za Logarithmic na Exponential: Kalkuleta za kisayansi zinashughulikia mahesabu ya logarithm asilia (ln) na msingi-10, pamoja na operesheni za exponential.
• Hesabu za Namba Changamani: Kwa masomo ya juu zaidi, kalkuleta hizi zinaweza kufanya mahesabu na namba changamani, muhimu katika uhandisi na fizikia.
• Kazi za Takwimu: Vipengele vya kuhesabu wastani, dhoto la kawaida, na maadili mengine ya takwimu vinajumuishwa, kurahisisha kazi kwa wanafunzi na wataalamu.
• Kazi za Kumbukumbu: Thamani zinaweza kuhifadhiwa na kurejeshwa, kurahisisha mchakato wa kushughulikia matatizo ya hatua nyingi.

Kalkuleta ya Kisayansi Mtandaoni 991 Plus inaongeza uwezo huu, ikitoa vipengele vya ziada kama mahesabu ya matrices, ujumuishaji, tofauti, na utatuzi wa milinganyo, na kuifanya kuwa chombo kamili kwa kazi za hesabu ngumu.

3. Kuelewa Kalkuleta ya Kisayansi 991 Plus

Kalkuleta ya Kisayansi 991 Plus ni kifaa cha hali ya juu kinachotumiwa na wanafunzi na wataalamu ulimwenguni kote. Vipengele kuu ni:

• Kiolesura cha Mtumiaji: Imetengenezwa kuwa rahisi kutumia, inaruhusu watumiaji kuvinjari kwa urahisi kazi ngumu.
• Kazi za Hisabati za Juu: Inaunga mkono kazi za ziada kama trigonometri hyperbolic, mahesabu ya vector, na regression ya takwimu, ambayo ni bora kwa masomo ya juu na kazi za kitaalamu.

Uwezo wake na uwezo wa kushughulikia operesheni ngumu hufanya iwe chaguo kuu kwa yeyote anayeshughulika na mahesabu makali.

4. Faida za Kutumia Kalkuleta ya Kisayansi Mtandaoni

Kalkuleta yetu ya kisayansi mtandaoni inatoa manufaa kadhaa kuliko kalkuleta za kawaida:

• Kupatika Kirahisi: Kupatikana wakati wowote na mahali popote kupitia tovuti yetu, inahakikisha watumiaji wanapata zana muhimu za hisabati popote walipo.
• Gharama Nafuu: Tofauti na kalkuleta ya kawaida, toleo letu la mtandaoni ni bure kutumia, hivyo kuokoa gharama ya kununua kifaa tofauti.
• Ufuatiliaji wa Kifaa: Iwe uko kwenye kompyuta, simu au kibao, kalkuleta yetu ya mtandaoni imesanifiwa kufanya kazi vizuri kwenye vifaa vyote.
• Visasisho vya Mara kwa Mara: Kwa jukwaa la mtandaoni, kazi mpya au sasisho zinaweza kuongezwa mara kwa mara, kuhakikisha kuwa kila wakati unapata zana za kisasa na kurekebisha hitilafu.

Zaidi ya hayo, Kalkuleta ya Kisayansi Mtandaoni 991 Plus inatoa kiolesura cha kirafiki, na kufanya iwe rahisi kwa watumiaji kuhamia kutoka kwa kalkuleta ya kawaida hadi toleo la mtandaoni bila kupoteza tija.

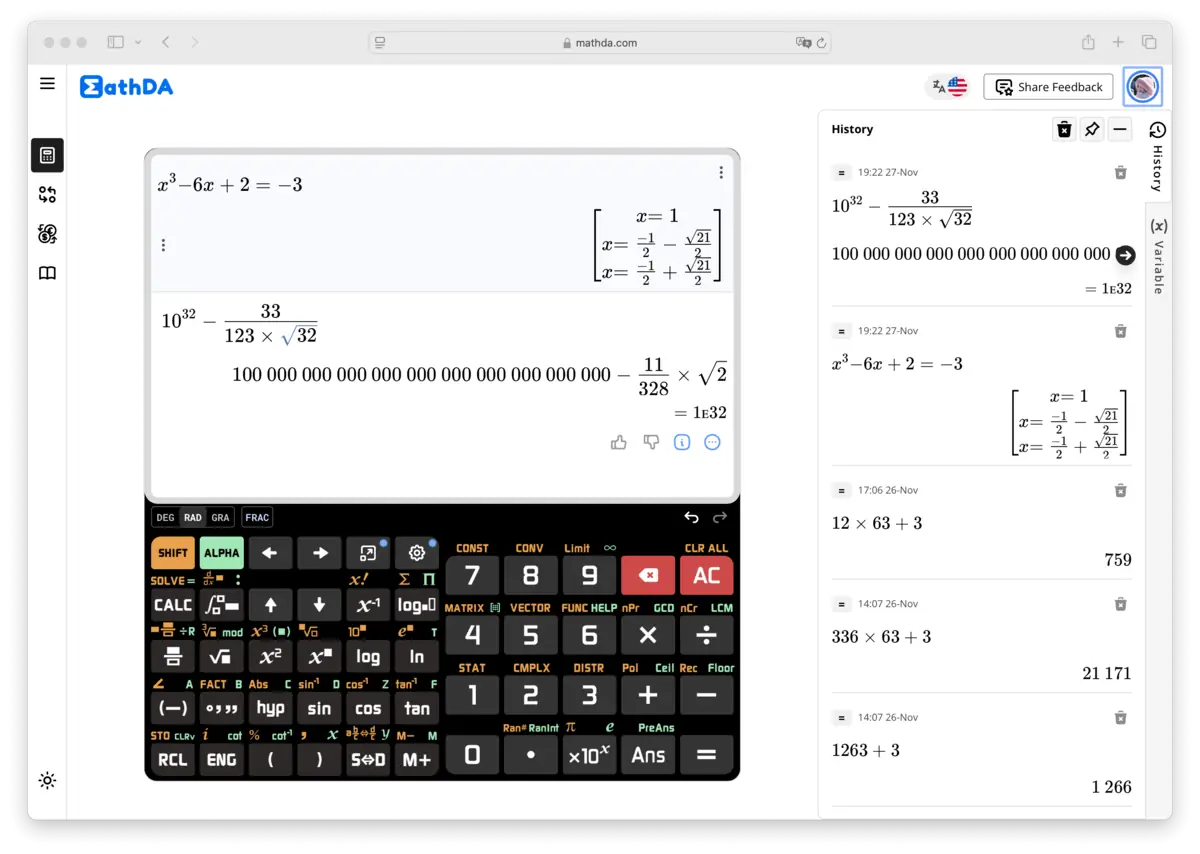
5. Matumizi ya Kalkuleta ya Kisayansi

Kalkuleta za kisayansi hutumika katika anuwai ya matumizi:

• Elimu: Ni muhimu kwa wanafunzi wa STEM, zikisaidia katika masomo kuanzia aljebra hadi fizikia. Kazi za juu za Kalkuleta ya Kisayansi Mtandaoni 991 Plus ni muhimu hasa kwa elimu ya juu, ambako utatuzi wa matatizo magumu unahitajika.
• Matumizi ya Kitaalamu: Katika uhandisi, fizikia, na uchambuzi wa takwimu, kalkuleta za kisayansi zinaruhusu utatuzi wa matatizo magumu unaohitajika katika nyanja nyingi za kiufundi. Vipengele vilivyoongezwa vya muundo wa 991 Plus huongeza zaidi msaada huu wa kitaalamu.
• Matumizi ya Kila Siku: Kalkuleta za kisayansi zinaweza kutumika kwa mahesabu ya nyumbani na ya kifedha, kama kuhesabu riba ya mkopo au ubadilishaji wa fedha, na kuzifanya kuwa muhimu hata nje ya mipangilio ya kitaaluma na kitaalamu.

Kwa kuwa na uwezo wa kutekeleza majukumu haya mtandaoni, inahakikisha watumiaji hawakosi zana zao muhimu za mahesabu, kuokoa muda na jitihada.

6. Vidokezo kwa Utumiaji wa Juu wa Kalkuleta ya Kisayansi Mtandaoni 991 Plus

Ili kufaidika zaidi na Kalkuleta ya Kisayansi Mtandaoni 991 Plus, zingatia yafuatayo:

• Jifunze Kiolesura: Pata muda wa kufahamu kazi zote zinazopatikana na njia za mkato ili kuboresha ufanisi wa mahesabu.
• Mazoezi ya Mara kwa Mara: Tumia kalkuleta mara kwa mara kuwa na ujuzi wa kuitumia kwa kazi mbalimbali.
• Tumia Rasilimali Mtandaoni: Pata mafunzo na miongozo inayoelezea jinsi ya kufanya mahesabu maalum, hasa kazi ngumu kama operesheni za matrix au ujumuishaji.

7. Hitimisho

Kalkuleta yetu ya kisayansi mtandaoni ni chombo chenye nguvu na cha kubadilika ambacho huleta uwezo wa kalkuleta ya kisayansi ya kimwili hadi kwenye urahisi wa kivinjari chako cha mtandao. Iwe wewe ni mwanafunzi, mhandisi, au mtu anayehitaji mahesabu sahihi, tunakuhimiza kuijaribu.

Kalkuleta ya Kisayansi Mtandaoni 991 Plus inatoa hata vipengele vya juu zaidi vinavyokidhi mahitaji makali ya mazingira ya kitaaluma na kitaalamu. Kwa upatikanaji, gharama nafuu, na uwezo wa kalkuleta yetu ya mtandaoni, hakuna haja ya kuwekeza katika kifaa cha kimwili. Gundua chombo hiki pamoja na rasilimali nyingine zinazopatikana kwenye tovuti yetu, na ugundue jinsi kalkuleta yetu ya kisayansi inaweza kusaidia malengo yako ya kielimu na kitaaluma.

Maswali Yanayoulizwa Mara kwa Mara (FAQ) Kuhusu Kalkuleta za Kisayansi Mtandaoni

1. Kalkuleta ya kisayansi mtandaoni ni nini?

Kalkuleta ya kisayansi mtandaoni ni chombo cha wavuti kinachoruhusu watumiaji kufanya mahesabu magumu ya kihisabati kama vile trigonometri, logarithm, viunzi, takwimu, na zaidi. Kwa kawaida huiga utendaji wa kalkuleta za kisayansi za kimaumbile.

2. Nitafikiaje kalkuleta ya kisayansi mtandaoni?

Unaweza kufikia kalkuleta ya kisayansi mtandaoni kupitia tovuti mbalimbali au programu. Tafuta tu "MathDA scientific calculator" katika kivinjari chako cha mtandao, na uchague moja inayokidhi mahitaji yako.

3. Je, ninahitaji kupakua au kusakinisha programu ili kuitumia?

Hapana, kalkuleta za kisayansi mtandaoni hufanya kazi moja kwa moja kwenye kivinjari chako bila kuhitaji upakuaji au usakinishaji.

4. Ni aina gani ya mahesabu naweza kufanya?

Unaweza kufanya aina mbalimbali za mahesabu, ikijumuisha:

• Hesabu za msingi (kujumlisha, kutoa, kuzidisha, kugawa)
• Kazi za trigonometri (sin, cos, tan, n.k.)
• Mahesabu ya logarithim na exponential
• Kazi za takwimu (wastani, dhoto la kawaida, regression, n.k.)
• Namba changamani na operesheni za matrix
• Ubadilishaji wa vitengo

5. Je, ni bure kutumia?

Kalkuleta yetu ya kisayansi mtandaoni ni bure kutumia.

6. Je, ninaweza kuchora grafu kwa kutumia kalkuleta ya kisayansi mtandaoni?

Ndiyo, kalkuleta zetu za kisayansi mtandaoni zinajumuisha uwezo wa uchoro. Unaweza kuchora grafu za kazi kwa uelewa bora.

7. Je, kalkuleta ya kisayansi mtandaoni ni sahihi?

Ndiyo, kalkuleta zetu za mtandaoni ni za usahihi wa hali ya juu.

8. Je, ninaweza kuitumia kwenye simu yangu au kibao?

Ndiyo, kalkuleta yetu ya kisayansi mtandaoni kawaida inakubalika kwa simu na inafanya kazi vizuri kwenye simu na vibao.

9. Je, kalkuleta za kisayansi mtandaoni ni salama?

Ndiyo, kalkuleta yetu ya kisayansi mtandaoni ni salama kutumia.

10. Je, inaweza kutatua milinganyo au kuonyesha suluhisho hatua kwa hatua?

Ndiyo, kalkuleta yetu ya mtandaoni inaweza kutatua milinganyo.

11. Je, kuna vikwazo vyovyote vya kutumia kalkuleta za kisayansi mtandaoni?

Kalkuleta yetu ya kisayansi mtandaoni ni yenye nguvu.

12. Je, wanafunzi wanaweza kuzitumia wakati wa mitihani?

Inategemea sheria za mtihani. Baadhi ya mitihani inaruhusu utumiaji wa zana za mtandaoni, wakati mingine inazuia ili kuzuia kudanganya.

13. Je, kalkuleta yetu ya kisayansi mtandaoni inafanya kazi kama kalkuleta halisi?

Ndiyo, kalkuleta yetu ya kisayansi mtandaoni inafanya kazi kama kalkuleta za kisayansi halisi, ikiega tabia ya kalkuleta za kimwili.