Base Number Calculation

CalcES allow you to perform calculation on DECIMAL, BINARY, OCTAL and HEXADECIMAL bases.

Press MODE , select BASE-N to enter Base-N Calculations mode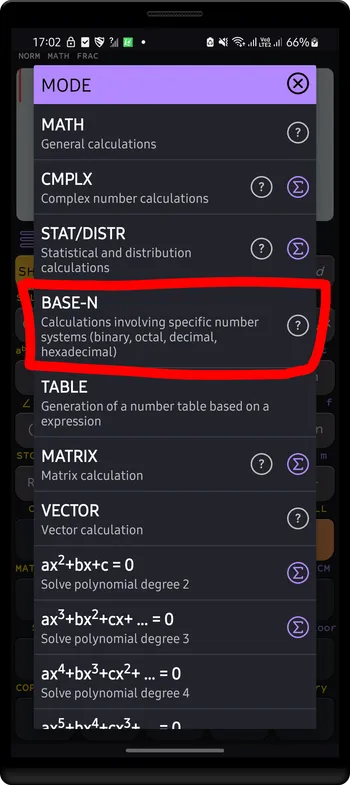
The Base-N display contains the current base and the bit size.

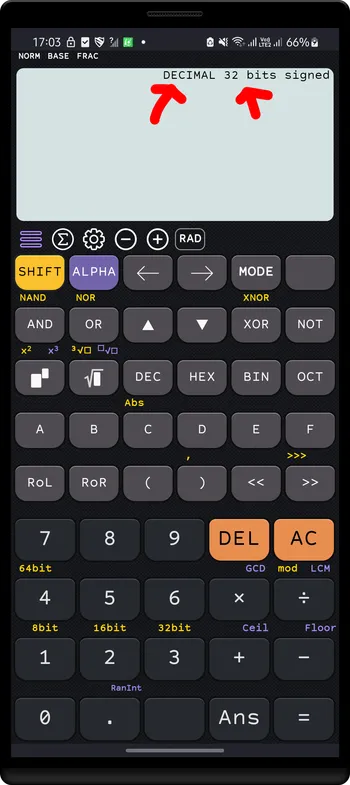
Base-n and bit size

Supported bases

BINARY: base 2, 01
OCTAL: base 8, 01234567
DECIMAL: base 10, 0123456789
HEXADECIMAL: base 16: 0123456789ABCDEF

Supported data types

8 bits (byte, int8)
16 bits (short, int16)
32 bits (int, int32)
64 bits (long, int64)

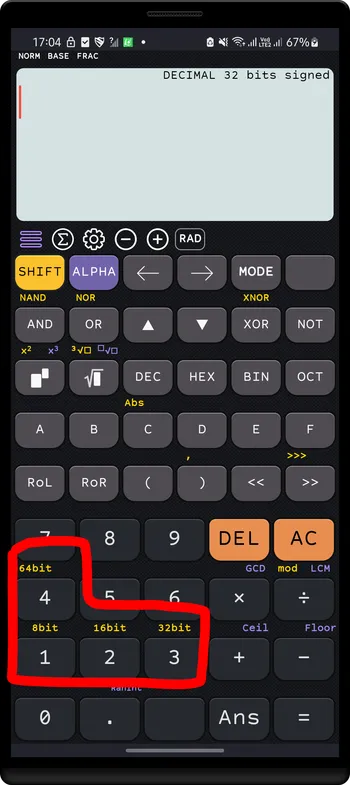
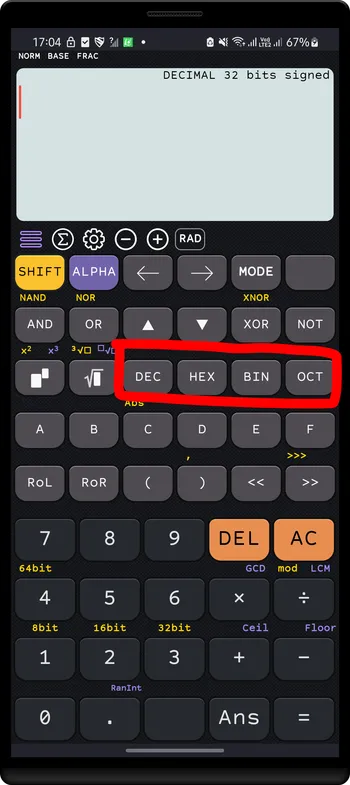
Converting from a base to another base

Example: Converting 542 (base 10) to base 2 (binary) and base 16 (hex)

Switch to DECIMAL base by pressing DEC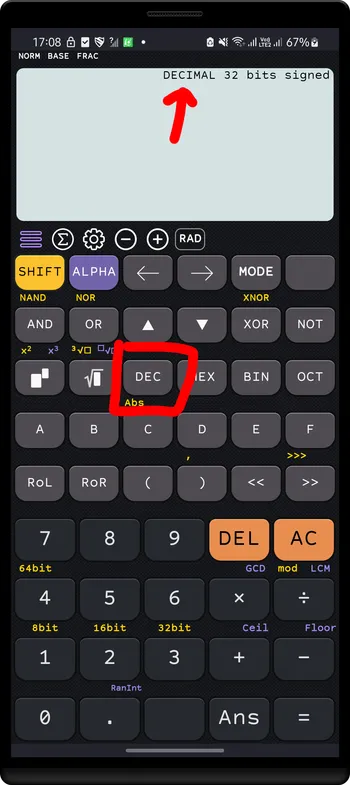
Enter 542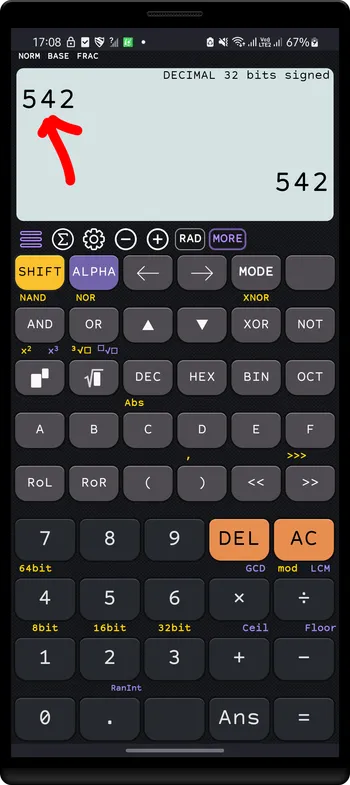
Press HEX to convert to hex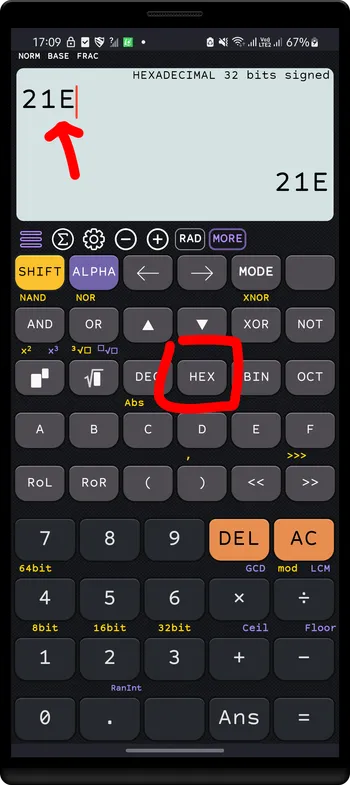
Press BIN to convert to binary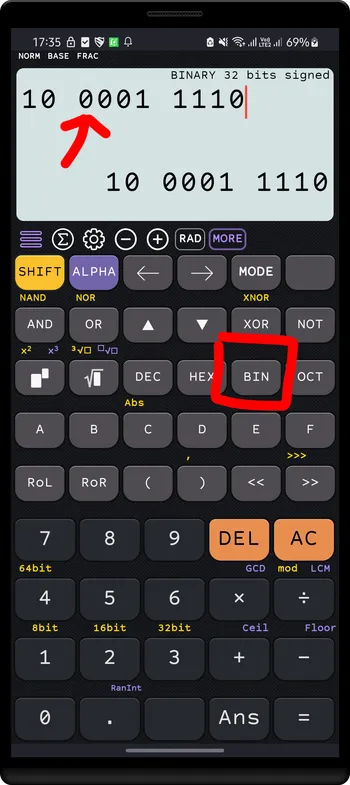

Operators

Arithmetic operators

Plus:

BINARY 16 bits signed

     1001
 +   1111
 = 1 1000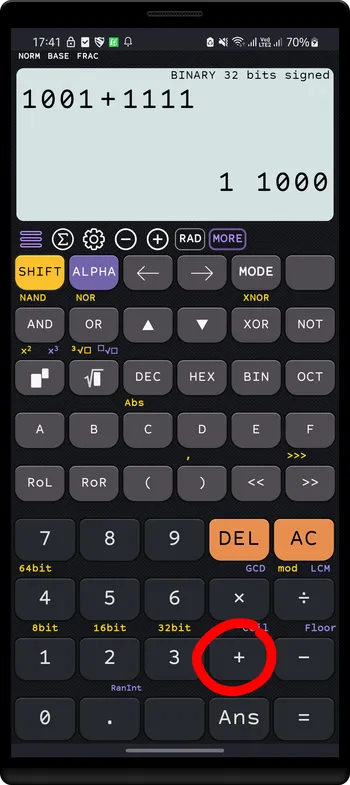

Subtract:

BINARY 16 bits signed

              1 0101
-            11 0100
=1111 1111 1110 0001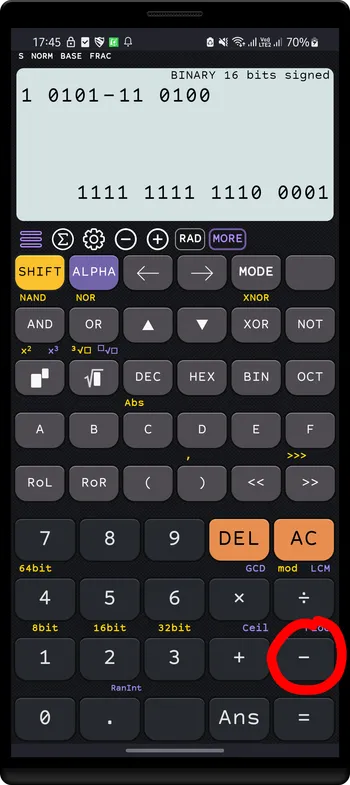

Multiply

HEXADECIMAL 16 bits
34E * FECB = 2DA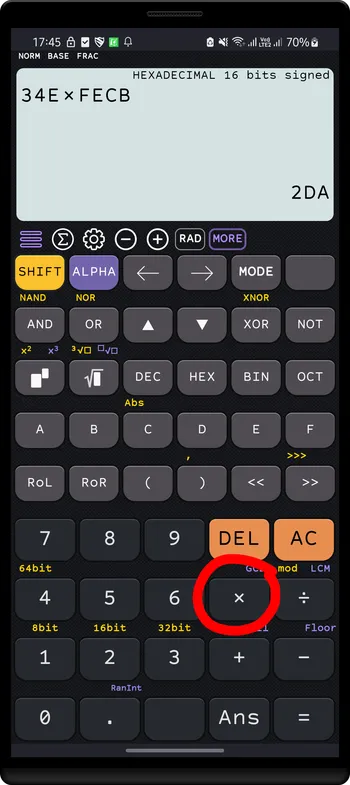

Divide

For non-integer value, (like 12.5), the calculator DOES NOT use an IEEE-754 format. Instead, it uses the following format:

12.52 (decimal) = 1100.1000 0101 0001 1110... (binary)

12.52 = 12 + 0.52

12 (decimal) = 1100 (binary)
   = 1*2^3 + 1*2^2 + 0*2^1 + 0*2^0 (decimal)
   = 8 + 4 + 0 + 0 (decimal)
   = 12 (decimal)

0.52 (decimal) = 0.1000 0101 0001 1110 (binary)
   = 1*2^-1 + 1*2^-6 + 1*2^-8 + 1*2^-12 ... (decimal)
   = 0.5 + 0.0015625 + 0.003 906 25 + ... (decimal)
   = 0.52

Example

BINARY 16 bits signed
1110 ÷ 110 = 10.0101 0101 0101 0101

(14 ÷ 6) = 2.333 333 ... (decimal)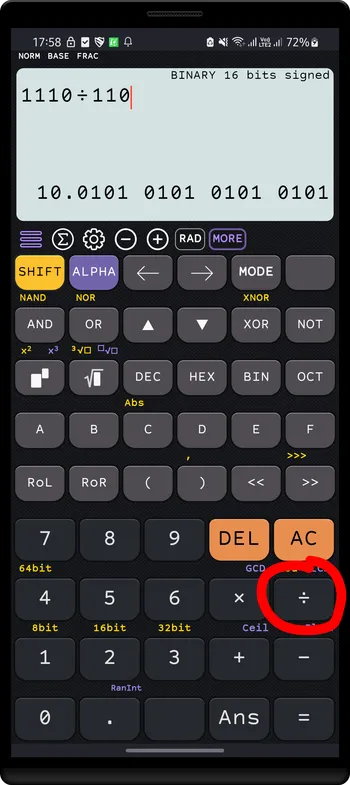

Mod

DECIMAL
63 mod 60 = 3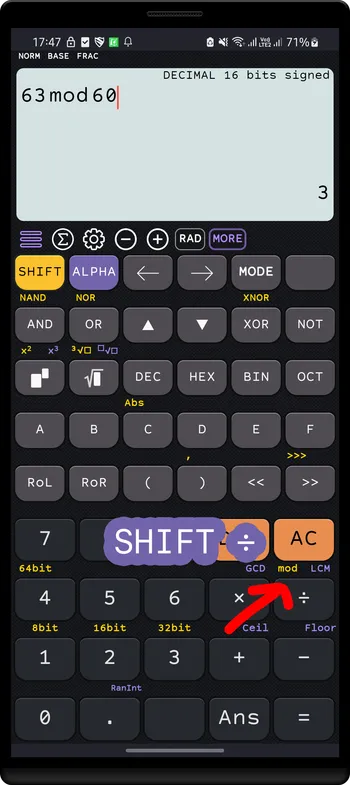

Logical operators

And

 1 0011
^1 0110
=1 0011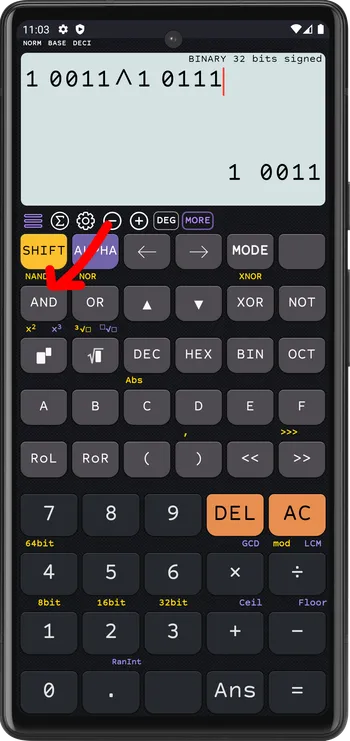

Nand

Or

  1 0011
v 1 0110
= 1 0111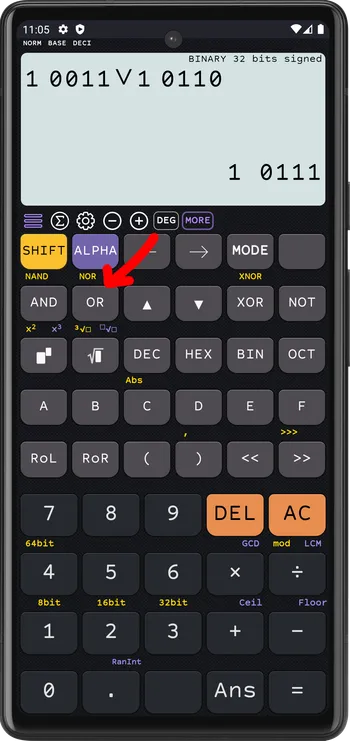

Nor

Xor

  1 0011
⊕ 1 0110
= 0 0101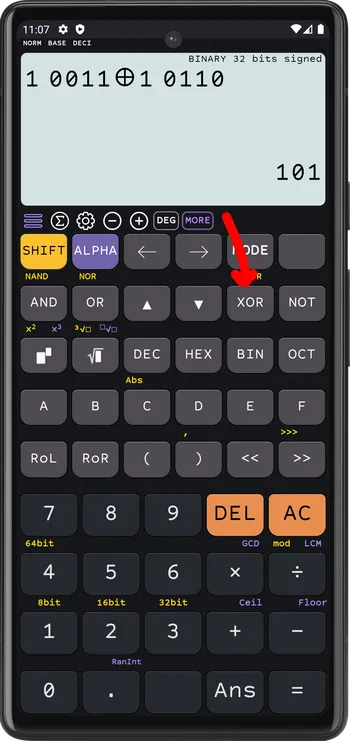

Nxor

Not

BINARY 8 bits signed

 ~1 0011 = 1110 1100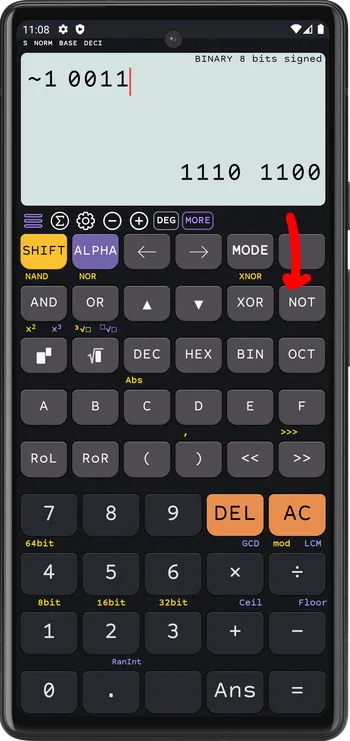

ShiftRight

When shifting right, the right most bit is lost and 0 is inserted on the left most.

1011 >>> 1  =  0101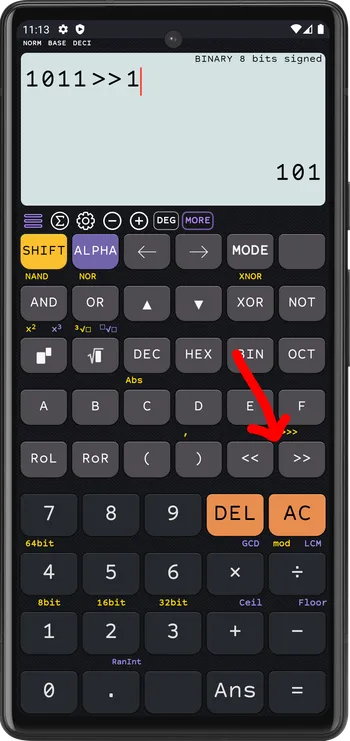

If a number is negative (encoded using two’s complement), then a right shift preserves the number’s sign

BINARY 8 bits signed

1101 1111 >> 1 = 1110 1111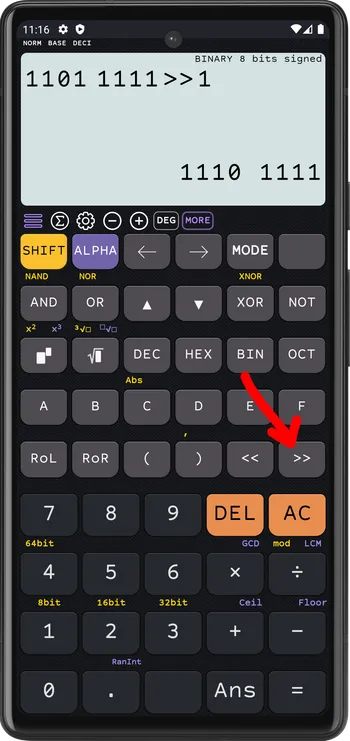

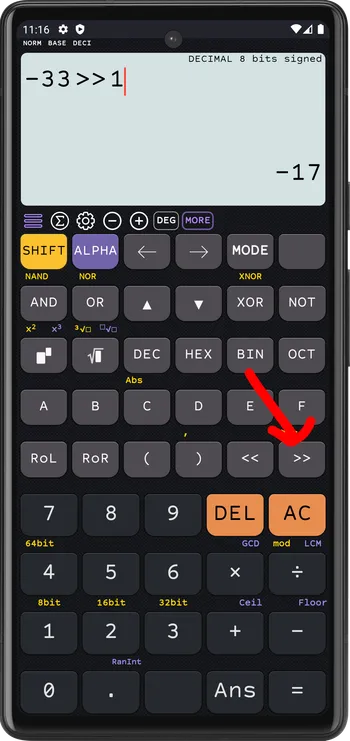
ShiftLeft

0010 << 1  =  0100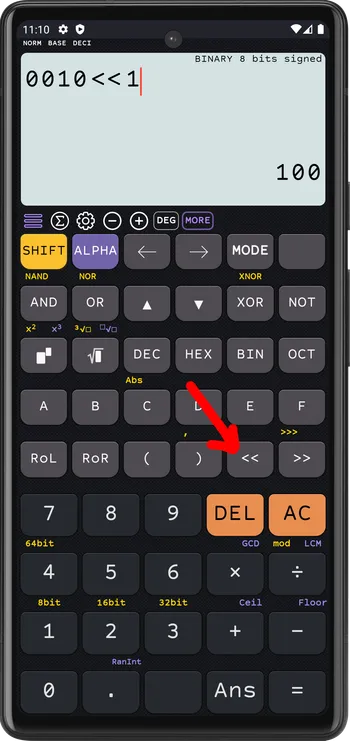

Logical functions

RotateLeft

BINARY 8 bits signed

 RotateLeft(1001 0111, 1)
=0010 1111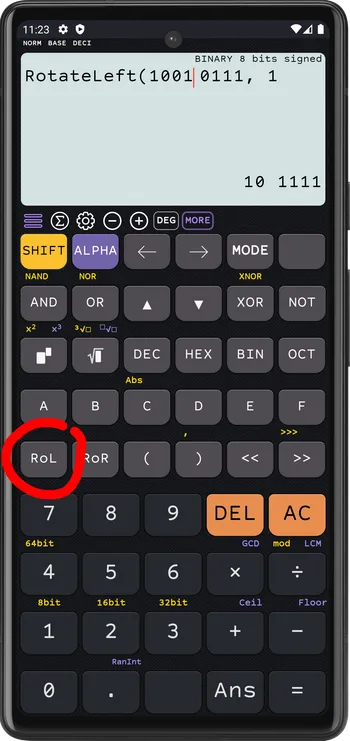

RotateRight

BINARY 8 bits signed

 RotateRight(1001 0111, 1)
=1100 1011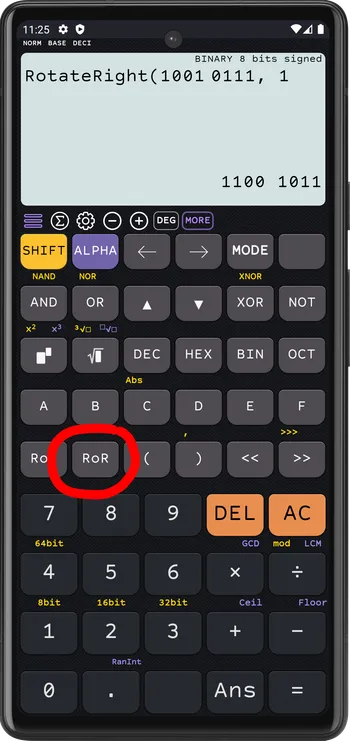

Floor

Ceil

Settings

Digit grouping format settings

The calculator allow to customize the digits grouping.

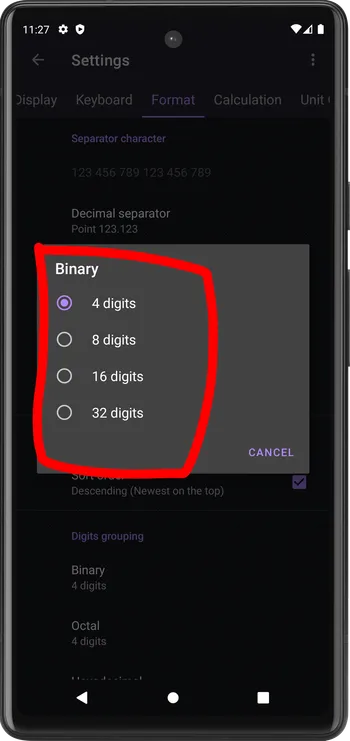
Example: the number 1001010010101001 can be formatted with 4, 9, 16 and 32 digits per group

1001 0100 1010 1001
10010100 10101001
1001010010101001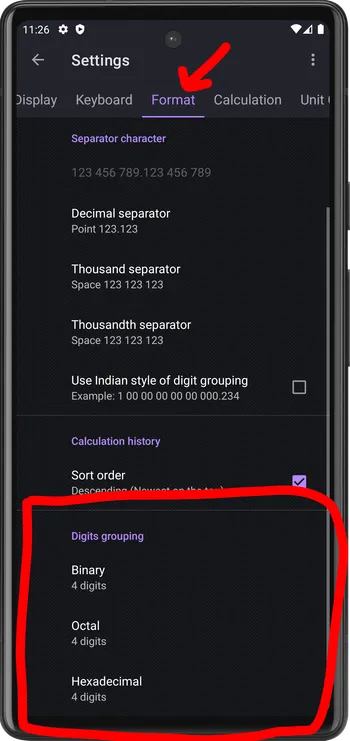

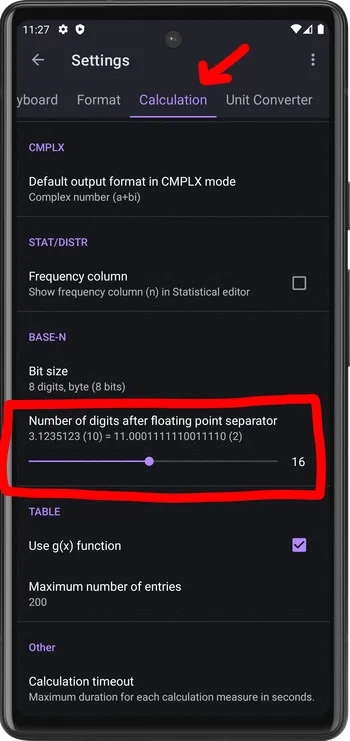
Fractional part precision of non-integer

This option allow to change the number of digits in fractional part of non-integer number.

3.1235123 (decimal) = 11.00011111 (binary)
3.1235123 (decimal) = 11.0001111110011110 (binary)
3.1235123 (decimal) = 11.00011111100111101000000010001001 (binary)